八年级数学上质量检测卷
班级： 学号： 姓名：
一、 选择题：（每题3分，共30分。）
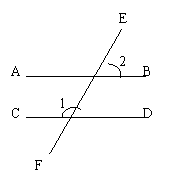1.如右图，AB∥CD，如果∠1是∠2的2倍，那么∠1等于（ ）
(A)60° (B)90° (C)120° (D) 150°
2.等腰三角形的两条边长是2和5，则它的周长是（ ）
A．12 C．9
B．14 D．9或14
3.∠B的相邻外角是100°，要使△ABC为等腰三角形，底角∠A的度数是( )
A．80° B. 50° C．80°或50° D．60°
4.下列判断正确的是（ ）
A．4a＞3a B．
≥a C．a＞—a D．a＞
5．一组数据x1，x2，x3，x4，x5的平均数是x，另一组数据2x1+5，2x2+5，2x3+5，2x4+5，2x5+5的平均数是（ ）
A ．x B． 2x C． 2x+5 D．10x+25
6．数据x，0，x，4，6，1中，中位数恰好是x，则整数x可能的值有（ ）个
A．1 B．2 C．3 D．4
7．已知不等式组 
的解集为X>2，则( )
x>m
A．m>2 B．m<2 C．m≥2 D．m≤2
8.一个直六棱柱的主视图和俯视图如右图所示，则它的左视图是( )
 | |||
 | |||
A B C D
9．不等式3x+1<m的正整数解是1，2，3，则整数m的最小值是（ ）
A．10 B．11 C．12 D．13
10．已知△ABC的三边分别为a，b，c，满足（a-24）2+（b-25）2+c2+49=14c，则△ABC的形状为（ ）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．形状不确定
二、 填空题（每小题3分，共30分）
11．满足不等式-1≤X<
的自然数x的个数为
。
12．已知直角三角形两条边的长分别为3cm和4cm，则第三边长为： cm。
13．等腰三角形一腰上的中线，将它的周长分成15cm和6cm两部分，则这个等腰三角形的底边上长是 cm。
14．数据1，3，2，5，4的方差是 ，标准差是 .
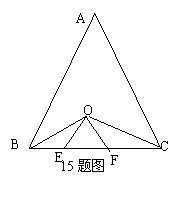
15．如图,已知在△ABC中,BC＝3，∠ACB和∠ABC的两条角平分线相交于点O，OE∥AB，OF∥AC，则△OEF的周长是＿＿＿＿。
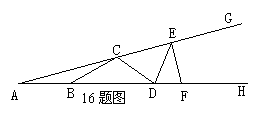
16．如图，C、E和B、D、F分别在∠GAH的两边上，且AB=BC=CD=DE=EF，若∠A=18°，则∠GEF的度数是________。
17.一鱼塘中大约有鱼2000尾，现分三次捕捞出30条鱼，称得其质量如下表，问鱼塘中所有鱼的质量大约是 千克.
| 第一次捕捞 | 第二次捕捞 | 第三次捕捞 | |
| 条数 | 8 | 10 | 12 |
| 平均质量 | 2.8千克 | 3.4千克 | 3.2千克 |
x-a≥0
18．已知关于x的不等式组 的整数解共有6个，则a的取值范围是
3-2x>-1
19．如图，直线a、b、c表示三条互相交叉的公路，
现要建一个货物中转站，要求它到三条公路的
距离相等，则可供选择的地址有 处。
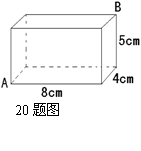
20.如图，长方体的长、宽、高分别为8cm，4cm，5cm。一只蚂蚁沿着长方体的表面从点A爬到点B。则蚂蚁爬行的最短路径的长是 cm
三、解答题（6分+10分+7分+8分+9分）
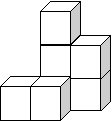21．画出下列几何体的三种视图．（6分）
22．解下列不等式（组），并分别在数轴上表示出它们的解集．（10分）
（1）
（2）
23．如图，AD是等腰△ABC的底边BC上的中线，过点D作DE∥AB，交AC于点E，判断△ADE是不是等腰三角形，并说明理由。（7分）
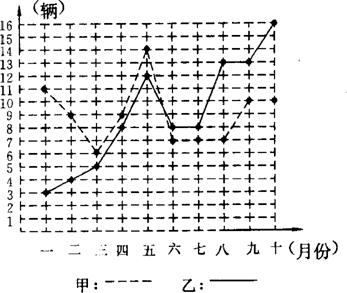24．某市甲、乙两个汽车销售公司，去年一至十月份每月销售同种品牌汽车的情况如图所示：
(1) 请你根据上图填写下表：(4分)
| 销售公司 | 平均数 | 方差 | 中位数 | 众数 |
| 甲 | 9 | |||
| 乙 | 9 | 17.0 | 8 |
（2）请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析：
①从平均数和方差结合看；（2分）
②从折线图上甲、乙两个汽车销售公司销售数量的趋势看（分析哪个汽车销售公司较有潜力）. （2分）
25．如图所示，细心观察图形，认真分析各式，解答问题。
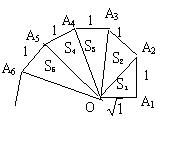
+1=2 ，S1=
；
+1=3，S2=
；
…
+1=4，S2=
；
…… ……
（1） 请用含有n（n是正整数）的等式表示上述变化规律。（2分）
（2） 推算出OA10的长。（3分）
（3） 求出S12 +S22+S32+……S102的值。（4分）