初二数学测试试卷

　　　　　　　　　　　　　　　 A卷

一、选择题：(分)

题号	1	2	3	4	5	6	7	8	9	10
答案

每题给出4个答案，其中只有一个是正确的，请把选出的答案编号填在上面的答题表中，否则不给分。

1. 以下列各组数为三角形的边长，能构成直角三角形的是

　(A)　 8，12，17； (B) 1，2，3； (C)　 6，8，10； (D) 5，12，9

2. 下列运算正确的是

　(A) 　(B) 　(C) 　(D)　

3. 下列说法中正确的是　

(A) 四边相等的四边形是正方形　　　　 (B) 等腰梯形的对角互补　　　　

4. 直角三角形两条直角边的长分别为8和6，则斜边上的高为

　　 (A) 2.4　　　(B) 4.8　　　　(C)　1.2　　　　(D)　 10

5. 将某个图形各点的纵坐标分别变为原来的2倍，横坐标分别变为原来的倍，则该图形被　　　　　　　　　　　

(A)　　　　横向压缩为原来的一半，纵向伸长为原来的2倍

(B)　　　　　横向伸长为原来的2倍，纵向压缩为原来的一半

(D)　　　　横向伸长为原来的2倍，纵向伸长为原来的2倍

6. 甲、乙两人相距42km，若想向而行，2h相遇；若同向而行，乙14h才能追上甲。则甲乙两人单位时间内各走

(A) 12km, 9km　 (B)　11km, 10km　 (C)　10km, 11km　 (D)　9km, 12km

7. 一段导线，在0℃时的电阻为2欧，温度每增加1℃，电阻增加0.008欧，那么电阻R欧表示为温度t℃的函数关系为

　(A) R=　(B)　R=　(C) R=　(D) R=

8. 下列图案是中心对称而不是轴对称的图案的个数是

H　　W　　 S　　Z

(A)　 1　 (B) 　 2　　(C) 　 3 　 (D)　 4　　　

9. 初二（8）班的43名同学在6月5日（世界环境日）调查了各自家庭丢弃废塑料袋的情况，统计结果如下：

每户居民丢弃废塑料袋的个数	2	3	4	5
户　数	4	16	15	8

根据调查数据，这43户居民丢弃废塑料袋的众数与中位数分别是：

（A）3， 3.5　　(B) 16，3.5　 (C)　16　，3　（D）3，4

10. 已知一次函数中，函数值y 随自变量x的增大而减小，那么m的取值范围是　　　　　　　　　　

（A）　　　　　 (B)　　　 (C) 　　 (D)　

二、填空题：(每空2分,共30分)

11. 9的算术平方根是______, 27的立方根是__________.

12. 的相反数是__________, =　　　 ,

13. 一个等腰三角形的腰长为13cm，底边长为10cm，则底边上的高为________

14. 若一个多边形外角和与内角和相等，则这个多边形是_________边形，

其内角和为________.

15. 正比例函数（k≠0）过点（－2，3），则正比例函数表达式为________, 　　　　　　　。

16. 点3, 到y轴的距离为　　　个单位，它关于原点对称的点的坐标为　　　　　　　　　　。

17. 直线与x、y轴的交点A、B的坐标为　　　　　，S_△_AOB= 　　　　.　　

18. 菱形两条对角线的长13cm , 12cm , 则这个菱形面积为　　　　 cm²。

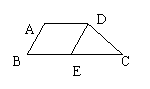19. 如图，在梯形ABCD中，AD∥BC，过D作DE∥AB

交BC于点E，若AD=6cm，ΔDCE的周长为21cm，那

么梯形的周长为　　　　　 cm 。

三、解答题：

20. 计算：（6分）

21. (10分)解方程组：① 　　　　　　　② 　　　　　　　　

22. （5分）一直线经过点(0, 3)和( 4), 画出其图像并求出其表达式.

23 .(5分) 对于边长为4的正△ABC，建立适当的直角坐标系(使三角形的一边在轴上)，写出各顶点的坐标。

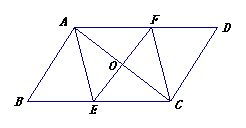
24.　(7分) 如图，平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E，F。问四边形AFCE是菱形吗?请说明理由.

25. （7分）某车间加工螺钉和螺母，当螺钉和螺母恰好配套（一个螺钉配一个螺母）时就可以运进库房．若一名工人每天平均可以加工螺钉120个或螺母96个，该车间共有工人81名．问应怎样分配人力，才能使每天生产出来的零件及时包装运进库房？

B卷

一．　　　　　填空（每题4分，共20分）

26．绝对值小于的所有实数的和为　　　　　　 .

27．已知平行四边形ABCD周长是54cm,AC和BD相交于O,且的周长大7cm,则CD的长是　　　　　　 .

28.已知聪明的同学你能不用计算器得出（1）　　　　；（2）　　　　；（3）　　　　 .

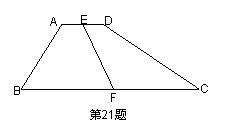29．如图，在梯形ABCD中，AD∥BC，∠B ＋∠C ＝90⁰，AD＝1，BC ＝3，E、F分别是AD、BC的中点，则EF＝　　　　　　

30.如果,则的形状是　　　　　　　．

二．解答题

31.正比例函数的图像经过P（1，-2）点，求当1≤X≤5时函数关系的最大值与最小值。

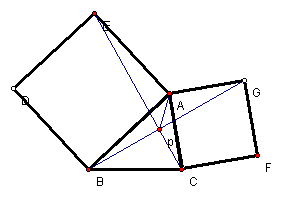
32.如图：在已知锐角三角形ABC的外面作正方形ABDE和正方形ACFG，EC和BG交于点P，求证：AP平分∠EPG。

33.已知点A（6，0），点P(x，y)在第一象限，且，设的面积为S

⑴求S关于x的函数表达式。

⑵求x的取值范围。

⑶求当S=12时，P点的坐标。

⑷画出函数图像。

初二数学测试试卷

H W S Z

H　　W　　 S　　Z