初二数学上学期第一次月考检测
满分：100分 时间：90分钟 命题人：王涛
一、填空题：（每题2分，共12×2分＝24分）
1．一棵树从离地面3米处断裂，树顶落在离树根部4米处，则树高
为 米。
2．以一个直角三角形的一条直角边为边长的正方形的面积为225，以这个
直角三角形的斜边为边长的正方形的面积为625，则以这个直角三角形的另一条直角边为边长的正方形的面积为 。
3．在△ABC中，AB=AC=17，BC=16，则高AD=
，S△ABC= 。
4．如图，一只蚂蚁在一个长方体表面沿图中所示方向从A爬
到G，已知AB=4cm，BC=5cm，CG=12cm，则蚂蚁爬过的最短路
程是 cm；
5．消防云梯的长度是25米,在一次执行任务时,它只能停在
离大楼7米远的地方,则云梯能达到大楼的高度是 米.
6．一根长24 cm的小木棒,分成三段,组成一个直角三角形,每段的长度都是偶数,则三段小木棒的长度分别是 cm 、 cm 、 cm。
7. 2-π的相反数是 ；
的倒数是 。
8. 若
=9，则m= ,若
= 3，则y = .
9. 比较大小：π 3.14 ；-
-。
10.
的算术平方根是
，
的立方根的相反数是 。
11. 的平方根是它的本身， _ ___的立方根是它本身。
12. 若实数a、b满足(a-2)
+
=0，则2b－a－1=
。
二、选择题：（每题3分，共10×3分＝30分）
13. 下列说法中，错误的是………………………………………………（ ）
A. △ABC中，若∠C=∠B + ∠A，则△ABC是直角三角形
B. △ABC中，a2=(b+c)(b-c), 则△ABC是直角三角形
C．△ABC中，∠A:∠B:∠C=3:4:5, 则△ABC是直角三角形
D. △ABC中，a:b:c=3:4:5, 则△ABC是直角三角形
14. 如果一个直角三角形的两条直角边扩大为原来的2倍，则斜边的长是原来的 倍。…………………………………………………………（ ）
A．1倍 B.2倍 C.3倍 D. 4倍
15. 在下列各数3.1415、0.…、
、
、
、
无理数的个数是………………………………………………………………………
( )
A 1 B 2 C 3 D 4
16. 下列各组线段中，不能作为直角三角形三边的是………………（ ）
A．12，15，20 B. 8，15，17 C．5，12，13 D. 7，24，25
17. 下列说法正确的有 个…………………………………………（ ）
①负数的立方根一定是负数；②实数都有平方根；③实数都有相反数；
④一个实数的绝对值一定大于0；⑤无理数就是带根号的数。
A 1个 B 2个 C 3个 D 4个
18. 下列各组数，都是无理数的一组是……………………………（ ）
A．-，
，
B. 
，0，π
C．
，0.3，
D. 
，
，
19. 若
=2，则（a+2）的平方根是……………………………（ ）
A. 2 B. 4 C. ±2 D. ±4
20. 一个自然数的算术平方根是x，则下一个自然数的算术平方根是………………………………………………………………………………（ ）
A．
+1 B. 
+1
C. 
D. x+1
21. 下面 A，B，C，D 四幅图中哪幅图是平移得到的？…………（ ）
22.下列运算正确的是………………………………………………（ ）
A 
B 
C 
D 
三、解答题（共46分）
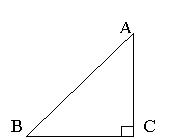23．已知，如图：Rt△ABC中，∠ACB＝90°，AB＝10cm，BC＝8cm。求Rt△ABC的面积（4分）
24．化简：（第1—4小题各4分，5、6小题各5分）
（1）
（2）
（3） 
（4）
（5）
（6）
25．求下列各式中的
值：（每题4′，共2×4′＝8′）
（1） 
＝27
（2）2＝50
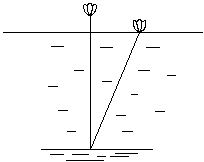
26．（8分）我国明朝数学家程大位曾提出过“荷花问题”：
平平湖水清可鉴，面上半尺生红莲；
出泥不染亭亭立，忽被强风吹一边，
渔人观看忙向前，花离原位二尺远。
能算诸君请解题，湖水如何知深浅？
| |
附加题（共20分）：观察下列各式及验证过程：
验证：
＝
＝
=
验证：
＝
验证：
＝
（1）按照上述三个等式及其验证过程的基本思路，猜想
的变形结果并进行验证。（8分）
（2）针对上述各式反映的规律，写出用n(n≥2的自然数)表示的等式，并进行验证。（12分）