等腰三角形单元学习评价
一、选择题
1．如果等腰三角形一个底角是30o，那么顶角是（ ）
（A）60o． （B）150o． （C）120o． （D）75o．
2、已知等腰三角形的周长为40ｃｍ，以一腰为边作等边三角形，其周长为45ｃｍ，则等腰三角形的底边长是（ ）A、5ｃｍ B、10ｃｍ C、15ｃｍ D、20ｃｍ
3．下列说法中，正确的是（ ）
（A）一个钝角三角形一定不是等腰三角形．（B）一个等腰三角形一定是锐角三角形．
（C）一个直角三角形一定不是等腰三角形．（D）一个等边三角形一定不是钝角三角形．
4、若△ABC的三边ａ、ｂ、ｃ满足
那么△ABC的形状是（ ）
A、等腰三角形 B、直角三角形 C、等边三角形 D、锐角三角形
5、等腰△ABC中，AC＝AB，两腰中线交于一点O，则AO与BC的关系是（ ）
A、相等 B、互相垂直 C、AO垂直平分BC D、AO、BC互相垂直
6.在等腰三角形中，AB的长是BC的2倍，周长为40，则AB的长为（ ）
（A）20． （B）16． （C）16或20． （D）以上都不对．
7．等腰三角形一腰上的高与另一腰的夹角为30o，则顶角的度数为（ ）
（A）60o． （B）120o． （C）60o或150o． （D）60o或120o．
8．等腰三角形一腰上的高与底边夹角为45o，则这个三角形是（ ）
（A）锐角三角形． （B）钝角三角形． （C）等边三角形． （D）等腰直角三角形．
9．两根木棒的长度分别是5cm和7cm，要选择第三根木棒，将它们钉成一个三角形，如果第三根木棒的长为偶数，那么第三根木棒长的取值情况有（ ）
（A）3种． （B）4种． （C）5种． （D）6种．
10．已知△ABC中，AB＝AC，且∠B ＝
，则的取值范围是（ ）
（A）≤45o． （B）0o＜＜90o．（C）＝90o． （D）90o＜＜180o．
11．等腰三角形一腰上的高与底边的夹角等于（ ）
（A）顶角．（B）顶角的一半 ．（C） 顶角的2倍． （D）底角的一半．
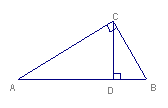
12、如图∠BCA=90，CD⊥AB，则图中与∠A互余的角有（ ）个
A．1个 B、2个 C、3个 D、4个
二、填空
13．(1)等腰三角形 、 、 互相重合．
（2）△ABC中，∠A=∠B=2∠C，那么∠C= 。
（3）在等腰三角形中，设底角为x°，顶角为y°，则用含x的代数式表示y，得y= ；用含y的代数式表示x，得x= 。
14．若一个等腰三角形有一个角为100o，则另两个角为 ．
15．等腰三角形中，两条边的长分别为4和9，则它的周长是 ．
16．已知等腰三角形一腰上的中线将它的周长分为9和12两部分，则腰长为 ，底边长为 ．
17．如果等腰三角形的三边长均为整数且它的周长为10 cm，那么它的三边为 ．
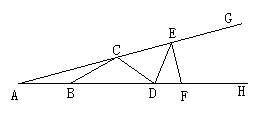
18．如图，C、E和B、D、F分别在∠GAH的两边上，且AB=BC=CD=DE=EF，若∠A=18°，则∠GEF的度数是（ ）
A．80° B．90° C．100° D．108°
三、作图题
20. 已知线段a,h,用直尺和圆规做等腰三角形ABC,底边BC=a,BC边上的高为h
（要求尺规作图，不写作法和证明）
└─────┘a
└──────┘h
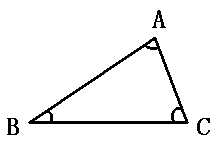
21、如图，已知在△ABC中，∠A=75º，
∠B=35º，∠C=70º，请将这个三角形分成两个等腰
三角形吗。（要求标出每个等腰三角形的内角度数）
三、解答题
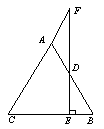22．已知AB＝AC，D是AB上一点，DE⊥BC于E，ED的延长线交CA的延长线于F，试说明△ADF是等腰三角形的理由．
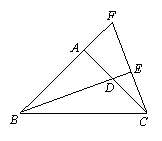23．如图，在△ABC中，∠BAC＝90o，AB＝AC，∠ABC的平分线交AC于D，过C作BD垂线交BD的延长线于E，交BA的延长线于F，求证：BD＝2CE．
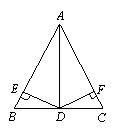24．如图，AB＝AC，BD＝DC，DE⊥AB，DF⊥AC，垂足分别是E，F．求证：DE＝DF．
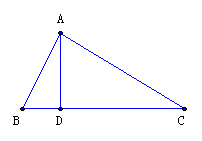
25如图，已知△ABC中，AD⊥BC，∠ABC＝2∠C，试说明AB＋BD＝CD的理由。
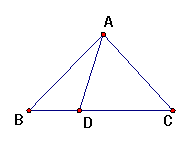
26、如图，在△ABC中，D是BC边上一点AD=BD，AB=AC=CD，求∠BAC的度数。
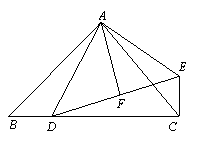27．如图，在△ABC中，已知AB＝AC，∠BAC＝90o，D是BC上一点，EC⊥BC，EC＝BD，DF＝FE．求证（1）△ABD≌△ACE；（2）AF⊥DE．
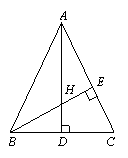28．如图，在△ABC中，AB＝AC，AD和BE是高，它们相交于点H，且AE＝BE．求证：AH＝2BD．
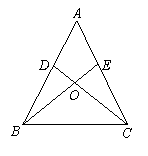29．在△ABC中，AB＝AC，BD＝DC，AD的延长线交BC于点E，求证：AE⊥BC，BE＝EC．
 |
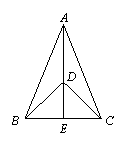30．已知：如图，AD＝AE，∠ADC＝∠AEB，BE与CD相交于O点．（1）在不添辅助线的情况下，请写出由已知条件可得出的结论（例如，可得出△ABE≌△ACD，∠DOB＝∠EOC，∠DOE＝∠BOC等．你写出的结论中不能含所举之例，只要求写出4个）．① ；② ；③ ；④ ．
（2）就你写出的其中一个结论给出证明．已知：如图AD＝AE，∠ADC＝∠AEB，BE与CD相交于O点．求证： ．
31.在ΔABC中，AB=AC
1（1），如图1，如果∠BAD=30°，AD是BC上的高，AD=AE，则∠EDC=__________
（2），如图2，如果∠BAD=40°，AD是BC上的高，AD=AE，则∠EDC=__________
（3），思考：通过以上两题，你发现∠BAD与∠EDC之间有什么关系？请用式子表示：____________________
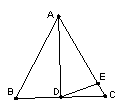
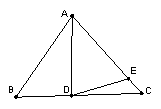
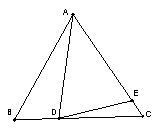2 如图3，如果AD不是BC上的高，AD=AE，是否仍有上述关系？如有，请你写出来，并说明理由
 |
（1） （2） （3）
32．已知等边△ABC和点P，设点P到△ABC三边AB、AC、BC的距离分别为h1，h2，h3，
△ABC的高为h．“若点P在一边BC上［如图（1）］，此时h3＝0可得结论：h1＋h2＋h3＝h．”请直接应用上述信息解决下列问题：当点P在△ABC内［如图（2）］，以及点P在△ABC外［如图（3）］这两种情况时，上述结论是否成立？若成立，请予以证明；若不成立，h1，h2，h3与h之间又有怎样的关系，请写出你的猜想，不需要证明．
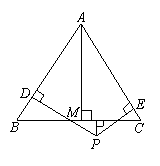
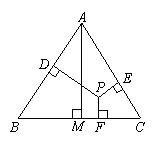
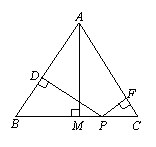
（1） （2） （3）
拓展思考：
已知：如图，点C为线段AB上一点，△ACM、△CBN是等边三角形，请说明AN=BM的理由。
现要求：（1）将△ACM绕C点按逆时针方向旋转180°，使A点落在CB上，请对照原题图在下面图中画出符合要求的图形（不写作法，保留作图痕迹）
（2）在（1）所得到的图形中，结论“AN=BM”是否还成立？请说明理由。
（3）在（1）得到的图形中，设MA的延长线与BN相交于D点，请你判断△ABD与四边形MDNC的形状，并说明你的结论成立的理由。