暑假作业：平行线
班级： 姓名： 学号：
一、填空题：
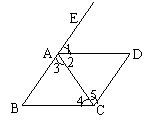
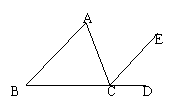
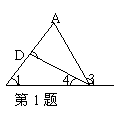1、如图，当直线BC，DC被AB所截时，∠1的同位角是 ，同旁内角是 ；当直线AB，AC被BC所截时，∠1的同位角是 ；当直线AB，BC被CD所截时，∠2的内错角是 。
 | |||||||||||
 | |||||||||||
 | |||||||||||
| |||||||||||
|
| ||||||||||
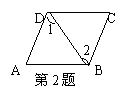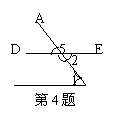
2、如图，∠1与∠2是直线 ，直线 被直线 所截而得的 角。
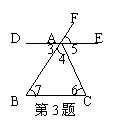
3、如图，指出两对同位角 ，两对内错角 ，五对同旁内角 。
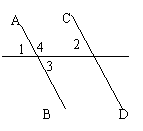
4、如图，（1）∠1的同位角是 ；（2）∠1与 是内错角；（3）∠1与∠3是 角；（4）若∠1＝∠4，则∠1与 也相等。
5、填空题：（1）如图，直线AB、CD被直线EF所截，如果∠1＝∠2，
则 理由是（ ）
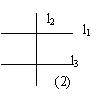（2）如图，l1⊥l2，l3⊥l2，则l1 l3。理由是 。
 |
(3)如图，∠2＝130°，∠3＝50°，则∠1＝ ， ∥ 。
理由是 。
6、如图，若∠1＝∠4，则 ∥ ；若∠2＝∠3，则 ∥ 。
7、填空题：
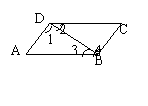
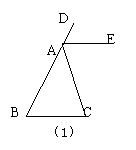
（1）如图AE∥BC，∠B＝50°，AE平分∠DAC，则∠DAC＝ ，∠C＝ 。
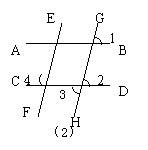
（2）如图AB∥CD，EF∥GH，∠1＝50°，则∠2＝ ，∠3＝ ，∠4＝ 。
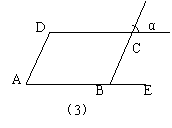
（3）如图，若AD∥BC，∠A＝∠α，则AB∥CD，说出说理过程。
∵AD∥BC（已知）， ∴∠A＝ 。（ ）
∵∠A＝∠α（ ），∠α＝ ，
|
∴AB∥CD（ ）。
8、如图（1）
|
|
|
（3）
|
（4）
|
（5）
9、已知：如图，∠1=78°，∠2=78°，∠3=78°，∠4=102°。
（Ⅰ）∵∠1=∠2=78°（已知），∴AB∥ ，
（Ⅱ）∵∠2=∠3=78°（已知），∴AB∥ ，
（Ⅲ）∵∠2+∠4=78°+102°=180°（已知），∴ ∥ （ ）
二、选择题：
1、下列图形中，∠1与∠2不是同位角的是――――（ ）
 | |||||
 | |||||
 | |||||
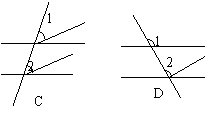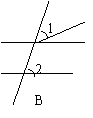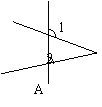2、∠1与∠2是两条直线被第三条直线所截的同位角，若∠1＝50°，则∠2为（ ）
（A）50° （B）130° （C）50°或130° （D）不能确定
3、一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那么这两次拐弯的角度应是――――（ ）
A、第一次向右拐40°，第二次向左拐140°B、第一次向左拐40°，第二次向右拐40°
C、第一次向左拐40°，第二次向左拐140°D、第一次向右拐40°，第二次向右拐40°
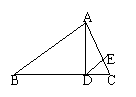
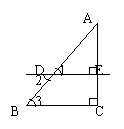
4、如图，AD⊥BC于点D，DE∥AB，则∠CDE与∠BAD的关系是――（ ）
A、相等 B、互余 C、互补 D、不能确定
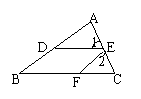5、在△ABC中，D、E、F分别为AB、AC、BC边上的点，
且DE∥BC，EF∥AB，那么下列结论中不正确的是―――（ ）
A、∠1＝∠C，∠2＝∠A B、∠1＝∠A，∠2＝∠C
C、∠ADE＝∠EFC D、∠B＝∠DEF
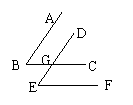
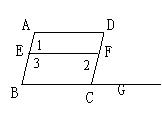6、如图，E、F分别是AB、CD上的点，G是BC延长线上一点，且∠B=∠DCG=∠D，则①∠1=∠2，②∠1=∠B，③∠A=∠3。上述结论中正确的是（ ）
A、只有① B、只有②
C、①和③ D、②和③
三、解答下列各题：
1、如图，Rt△ABC中，∠C＝Rt∠，DE⊥AC，交AB于点D。
（1） 说出当BC、DE被AB所截时，∠3的同位角、内错角和同旁内角。
（2）试说明∠1＝∠2＝∠3的理由。
2、如图，∠ABC＝∠DEC，BP平分∠ABC，EF平分∠DEC，试找出图中的各组平行线。
 |
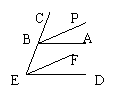3、如图，△ABC中，∠A＝∠B，若CE平分外角∠ACD，则能CE∥AB，试说明理由。
（填空）理由：
∵∠A＝∠B（ ）
∴∠ACD＝∠A＋ （ ）＝2∠B。
∵CE平分∠ACD（ ）
∴∠ACD＝ ∠ECD（ ）
∴∠B＝∠ECD，
∴CE∥AB（ ）。
4、下面的说理是否正确，若不正确，请改正。
已知AB∥DE，∠B=∠E，说明BC∥EF。
解：∵AB∥DE
∴∠B=∠DGC (同位角相等，两直线平行)
∵∠B＝∠E
∴∠DGC＝∠E
∴BC∥EF（两直线平行，同位角相等）
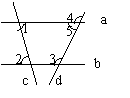
5、如图，已知a∥b，c、d都是a、b的截线，∠1＝80°，∠5＝70°。∠2、∠3、∠4各是多少度？为什么？
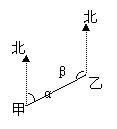
6、如图，在甲、乙两地之间要修一条公路，从甲地测得公路的走向是北偏东55°，如果甲、乙两地同时开工，那么在乙地公路按∠β是多少度施工，才能使公路准确接通？
7、如图，已知直线l和点P，过点P作直线l的平行线。(不写作法，求出这两条直线间的距离)
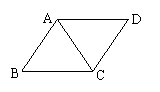8、如图，AB∥CD，AD∥BC，请过点B作AD与BC之间的垂线段，并量出AD与BC之间的距离。
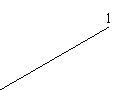
9、已知直线l如图，求作一条直线m，使l与m的距离为2cm，（只需作一条，要求写出作法）。
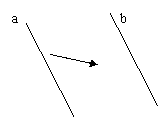10、如图，直线b是直线a沿箭头方向平移所得的像，请你测量a，b之间的距离。
11、下面的说法是否正确，若不正确，请改正。
两条平行线之间的距离是指：一条平行直线上的任一点到另一条平行直线上一点的距离。
 |
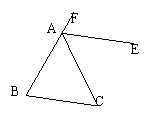12、已知AE是∠FAC的平分线，∠B＝∠C＝40°，试说明AE∥BC。
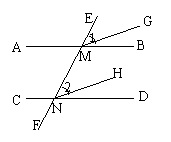13、如图，已知AB∥CD，直线EF分别截AB、CD于点M、N，MG、NH分别是∠EMB与∠END的平分线。试说明MG∥NH。
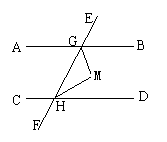14、已知AB∥CD，EF交AB、CD于G、H，若∠BGH和∠DHG的平分线交于点M，试判断GM和HM是否垂直，并说明理由。