暑假作业：特殊三角形测试题
班级： 姓名： 学号：
一、填空题：
1、（1）等腰三角形中，如果底边长为6，一腰长为8，那么周长是 。
（2）如果等腰三角形有一边长是6，另一边长是8，那么它的周长是 ；如果等腰三角形的两边长分别是4、8，那么它的周长是 。
（3）等腰三角形的对称轴最多有 条。
2、（1）等腰三角形的顶角平分线、 、 互相重合。
（2）等腰三角形有一个角是120°，那么其他两个角的度数是 和 。
（3）△ABC中，∠A=∠B=2∠C，那么∠C= 。
（4）在等腰三角形中，设底角为x°，顶角为y°，则用含x的代数式表示y，得y= ；用含y的代数式表示x，得x= 。
3、（1）在△ABC中，∠A的相邻外角是110°，要使△ABC是等腰三角形，则∠B= 。
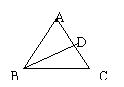（2）如果等腰三角形底边上的高线和腰上的高线相等，则它的各内角的度数是
。
（3）在一个三角形中，等角对 ；等边对 。
（4）如图，AB=AC，BD平分∠ABC，且∠C=2∠A，
则图中等腰三角形共有 个。
4、（1）等边三角形的三条边都 ，三个内角都 ，且每个内角都等于 。
（2）等边三角形有
条对称轴。
（3）等边三角形的 、 、 互相重合。
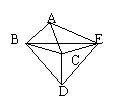
（4）如图，△ABC和△BDE都是等边三角形，如果∠ABE=40°，
那么∠CBD= 度。
5、（1）在△ABC中，若∠A=∠B+∠C，则△ABC是 。
（2）在△ABC中，∠C=90°，∠A =2∠B，则∠A= ，∠B= 。
（3）在△ABC中，若∠A∶∠B∶∠C=1∶2∶3，则△ABC是 三角形。
（4）直角三角形两锐角之差是12度，则较大的一个锐角是 度。
6、（1）等腰三角形的底角为15度，腰长为2a，则三角形的面积为 。
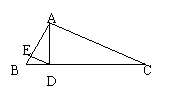（2）已知：如图，∠BAC=90°，∠C=30°，
AD⊥BC于D，DE⊥AB于E，BE=1，BC= 。
（3）在△ABC中，如果∠A+∠B=∠C，且AC=
AB，
则∠B= 。
7、（1）勾股定理说的是 。
（2）直角三角形的两边长分别是3cm、4cm，则第三边长是 。
（3）直角三角形的周长是24cm，斜边上的中线长为5cm，则此三角形的面积是 。
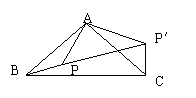（4）如图，△ABC是Rt△，BC是斜边，P是三角形内一点，将△ABP绕点
A逆时针旋转后，能与△ACP′重合，如果AP=3，那么PP′的长等于 。
8、（1）如果三角形中 等于 ，那么这个
三角形是直角三角形， 所对的角是直角。
（2）在△ABC中，已知AB=40，BC=41，AC=9，则∠BAC= 度。
9、（1）如图1，已知AB⊥AC，AC⊥CD，垂足分别是A，C，AD=BC。由此可判定全等的两个三角形是△ 和△ 。
（2）如图2，已知BD⊥AE于B，C是BD上一点，且BC=BE，要使Rt△ABC≌Rt△DBE，应补充的条件是∠A=∠D或 或 或 。
（3）如图3，在△ABC中，AD⊥BC于D，AD与BE相交于H，且BH=AC，DH=DC，那么∠ABC= 度。
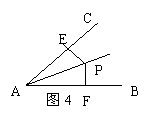
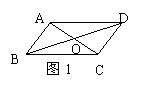
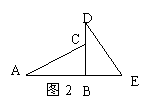
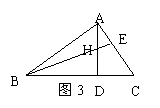（4）如图4，点P是∠BAC内一点，且P到AC，AB的距离PE=PF，则△PEA≌△PFA的理由是
。
二、选择题：
1、（1）如果△ABC是等腰三角形，那么它的边长（或周长）可以是（ ）
A、三条边长分别是5，5，11 B、三条边长分别是4，4，8
C、周长为14，其中两边长分别是4，5 D、周长为24，其中两边长分别是6，12
（2）等腰三角形一边长为2，周长为5，那么它的腰长为（ ）
A、3 B、2 C、1.5 D、2或1.5
2、（1）等腰三角形的一个外角为140°，那么底角等于（ ）
A、40° B、100° C、70° D、40°或70°
（2）等腰三角形一腰上的高线与底边的夹角等于（ ）
A、顶角 B、底角 C、顶角的一半 D、底角的一半
（3）在等腰三角形ABC中，∠A与∠B度数之比为5∶2，则∠A的度数是（ ）
A、100° B、75° C、150° D、75°或100°
（4）等腰三角形ABC中，AB=AC，AD是角平分线，则“①AD⊥BC，②BD=DC，
③∠B=∠C，④∠BAD=∠CAD”中，结论正确的个数是（ ）
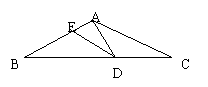A、4 B、3 C、2 D、1
3、如图，在△ABC中，AB=AC，∠BAC=108°，∠ADB=72°，
DE平分∠ADB，则图中等腰三角形的个数是（ ）
A、3 B、4 C、5 D、6
4、（1）如果三角形的一个角等于其他两个角的差，那么这个三角形是（ ）
A、锐角三角形 B、直角三角形 C、钝角三角形 D、以上都错
（2）如果三角形的三个内角的比是3∶4∶7，那么这个三角形是（ ）
A、锐角三角形 B、直角三角形 C、钝角三角形 D、锐角三角形或钝角三角形
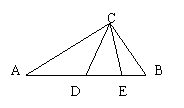
（3）△ABC中，如果两条直角边分别为3，4，则斜边上的高线是（ ）
A、
B、
C、5
D、不能确定
（4）如图，△ABC中，∠ACB=Rt∠，在AB上截取AE=AC， BD=BC，则∠DCE等于（ ）
A、45° B、60° C、50° D、65°
5、（1）已知等腰三角形一腰上的高线为腰长的一半，那么这个等腰三角形的一个底角为（ ）
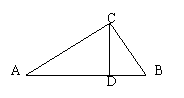A、15°或75° B、15° C、75° D、150°或30°
（2）如图，在△ABC中，∠ACB=90°， CD⊥AB于D，∠A=30°，则AD等于（ ）
A、4BD B、3BD C、2BD D、BD
（3）如图，EA⊥AB，BC⊥AB，AB=AE=2BC，D为AB的中点，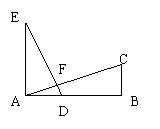
有以下
判断：①DE=AC；②DE⊥AC；③∠CAB=30°；
④∠EAF=∠ADE；其中正确结论的个数是（ ）
A、1 B、2 C、3 D、4
6、已知有不重合的两点A和B，以点A和点B为其中两个顶点作位置不同的等腰直角三角形，一共可以作出（ ）
A、2个 B、4个 C、6个 D、8个
7、（1）边长分别是下列各组数的三角形中，能组成直角三角形的是（ ）
A、5，10，13． B、5，7，8。 C、7，24，25。 D、8，25，27。
（2）满足下列条件的△ABC，不是直角三角形的是（ ）
A、b2=a2-c2 B、∠C=∠A-∠B C、∠A∶∠B∶∠C=3∶4∶5 D、a∶b∶c=12∶13∶5
8、下列条件中，不能判定两个直角三角形全等的是（ ）
A、一条直角边和一个锐角分别相等 B、两条直角边对应相等
C、斜边和一条直角边对应相等 D、斜边和一个锐角对应相等
三、解答下列各题：
1、已知等腰三角形的腰长是底边的3倍，周长为35cm，求等腰三角形各边的长。
 |
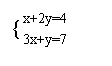2、已知等腰三角形的底边和一腰长是方程组 的解，求这个三角形的各边长。
 |
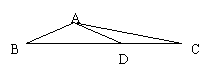3、如图，已知△ABC中，D在BC上，AB=AD=DC，∠C=20°，求∠BAD。
 |
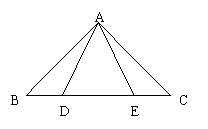4、如图，已知△ABC中，点D、E在BC上， AB=AC，AD=AE。
请说明BD=CE的理由。
 |
5、如图，已知∠EAC是△ABC的外角，∠1=∠2，AD∥BC，请说明AB=AC的理由。
6、如图，在等边△ABC中，D是AC的中点，E是BC延长
线上一点，且CE=CD，请说明DB=DE的理由。
7、若a、b、c为△ABC的三边，且a2+b2+c2=ab+bc+ca，请说明△ABC是等边三角形。
 |
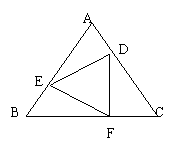8、已知，如图，△ABC是正三角形，D，E，F分别是各边上的一点，
且AD=BE=CF。请你说明△DEF是正三角形。
9、在一个直角三角形中，如果有一个锐角为30度，且斜边与较小直角边的和为18cm，求斜边的长。
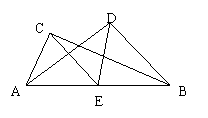10、如图，△ABC和△ABD中，∠C=∠D=Rt∠，E是BC边上
的中点。请你说明CE=DE的理由。
11、在△ABC中，∠C=Rt∠，BC=a，AC=b，AB=c。
（1）a=9，b=12，求c；（2）a=9，c=41，求b；（3）a=11，b=13，求以c为边的正方形面积。
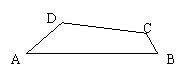12、如图，在四边形ABCD中，AB=8，BC=1，∠DAB=30°，
∠ABC=60°，四边形ABCD的面积为5
，求AD的长。
13、在直角三角形中，如果两直角边之和为17，两直角边之平方差为119，求斜边的长。
14、根据三角形的三边a，b，c的长，判断三角形是不是直角三角形：
（1）a=11，b=60，c=61； （2）a=
，b=1，c=
；
15、在△ABC中，三条边长分别为2n2+2n，2n+1，2n2+2n+1（n＞0）。那么△ABC是直角三角形吗？请说明理由。
 |
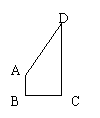16、如图，已知一个四边形的四条边AB，BC，CD和DA的长分别是3，4，
13和12，其中∠B=90°，求这个四边形的面积。
 |
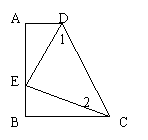17、如图，AD∥BC，∠A=90°，E是AB上一点，∠1=∠2，AE=BC。
请你说明∠DEC=90°的理由。
18、如图，AD=BC，DE⊥AC，BF⊥AC，E，F是垂足，DE=BF。请你说明（1）∠DAE=∠BCF；（2）AB∥CD成立的理由。