第六章 图形与坐标
班级 姓名 学号
一、 选择题（每题3分，共30分）
1．电影票上8排12号简记为（ ）
A．812 B．128 C．（8，12） D．（12，8）
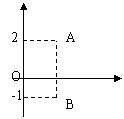2．如图，点A与点B的横坐标（ ）
A．相同 B．相隔3个单位长度
C．相隔1个单位长度 D．无法确定
3．在直角坐标系中，点A（2，1）向左平移2个
单位长度后的坐标为（ ）
A．（4，1） B．（0，1） C．（2，3） D．（2，-1）
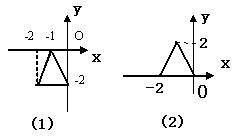4．观察图（1）与（2）中的两个三角形，可把（1）中的三角形的三个顶点，怎样变化就得到（2）中的三角形的三个顶点（ ）
A．每个点的横坐标加上2 B．每个点的纵坐标加上2
C．每个点的横坐标减去2
D．每个点的纵坐标减去2
5．已知点P的坐标为（-3，-4），则点P到y轴的距离为（ ）
A．-3 B．3 C．4 D．-4
6．若点P在x轴的上方和y轴的左方，到每条坐标轴的距离为4，则点P的坐标为（ ）
A．（4，4） B．（-4，-4） C．（-4，4） D．（4，-4）
7．点M（-1，2）与点N关于y轴对称，则点N的坐标为（ ）
A．（1，-2） B．（-1，-2） C．（1，2） D．（2，-1）
8．在平面直角坐标系中，点P（-2，3）向右平移3个单位后的坐标为（ ）
A．（3，6） B．（1，3） C．（1，6） D．（3，3）
9．∆ABC各顶点的横坐标不变，纵坐标分别加3，连结三个点所成三角形是由∆ABC（ ）
A．向左平移3个单位所得 B．向右平移3个单位所得
C．向上平移3个单位所得 D．向下平移3个单位所得
10．已知正方形OABC各顶点坐标为O（0，0），A（1，0），B（1，1）C（0，1），若P为坐标平面上的点，且∆POA、∆PAB、∆PBC、∆PCO都是等腰三角形，问P点可能的不同位置数是（ ）
A．1 B．5 C．9 D．13
二、填空题（每题3分，共30分）
11．点P（a,b）在x轴上，则a ,b .
12.点P（3a-9,a+1）在第二象限，则a的取值范围为 。
13．小明站在旗杆的北偏东40°方向上，且距离旗杆80米，则旗杆应在小明
位置。
14．点M（3，-2）关于x轴对称点的坐标为 。
15．在直角坐标系中，若一个正方形，每个顶点到横轴、纵轴的距离都是6，则此正方形的四个顶点坐标分别为 。
16．若点A（x，0）与点B（2，0）的距离等于3，则x= .
17.对于边长为4的正∆ABC，以BC所在直线为x轴，以边BC的中垂线为y轴建立直角坐标系，那么点A的坐标是 。
18．某市地图上有A和B两个生活小区，A区在B区的西南方向，且相距B区2000米，小华以B区为坐标原点，以正东方向为x轴正方向，以正北方向为y轴正方向，以100米为单位长度建立直角坐标系，则点A区坐标为 。
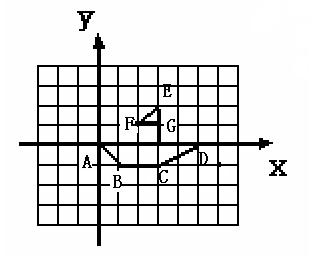
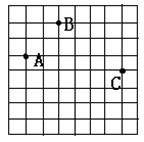19．如图所示，小明告诉小华图中A、B两点坐标分别是（-3，6），（3，5），小华立刻说出了点C的坐标，则他说的点C的坐标为
。
20．已知点A（a，6）和B（2，6），且AB平行于x轴，则a的取值范围为 。
三、解答题（21题、22题每题6分，23—26题每题7分，共40分）
21．建立适当的平面直角坐标系，并在图中描出坐标是（2，3），（-2，3），（3，-2），（5，1），（0，-4），（-3，0）的点。
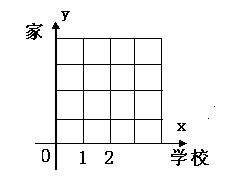
22．如图，小明从家到学校要穿过一个居民小区，小区的道路均是正南或正东方向，请你帮小明设计一条从家到学校的路线，并在图上画出，用坐标描述他的行走路线。
23．在平面直角坐标系中，将坐标是（-5，0），（-4，-2），（-3，0），（-2，-2），（-1，0）的点用线段依次连接起来，形成图案I，
（1）作出该图案关于y轴对称的图案II；
（2）将所得的图案II沿x轴向上翻折180°后得到一个新的图案III，试写出它的各顶点坐标；
（3）观察图案I与III，比较各自顶点的坐标和图案位置，你能得到什么结论？
24．试判断以A（-1，-1），B（5，-1），C（2，2）为顶点的三角形的形状。
25．如图所示是一艘船在平面直角坐标系内的位置，
（1）写出图中所标出的各个点的坐标；
（2）如果船朝东航行6个单位长度，再向北平移4个单位长度，则变化后船所在位置的各点坐标为怎样？
26．已知在直角坐标系中，点A（4，0），点B（0，3），若有一个直角三角形与Rt∆ABO全等，且它们有一条公共边，请写出这个直角三角形未知顶点的坐标。（不必写出计算过程）
四、附加题（每题10分，共20分）
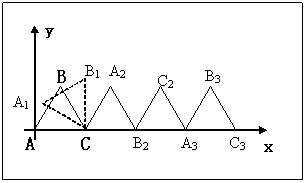
27．如图所示，正∆ABC在平面直角坐标系中按顺时针方向滚动，已知点A与坐标原点重合，正∆ABC的边长为2，
（1）求出点B及点C的坐标；
（2）把∆ABC绕点C旋转30°后，点B所在位置的坐标是什么？
（3）三角形ABC滚动360°后，点A，点B、点C分别位于什么位置？
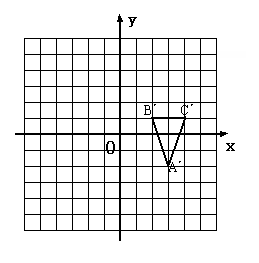
28．∆ABC先向下平移3个单位长度，再绕原点顺时针旋转180°，得如图所示的∆A´B´C´，试确定∆ABC的位置，并定出顶点坐标。
 |