八年级数学第一学期期中知识评价

八年级数学第一学期期中知识评价

姓名：　　　　　 　班级：　　　　  得分：　　　　　

一、选择题（30）

1、不是由两直线平行直接得到的结论是　　　　（　　）

A、内错角相等　B、同位角相等　C、对顶角相等　D、同旁内角互补

2、等腰三角形的一个外角是130°，则它的底角等于（　　 ）

A、50°　　　B、65°　　　　C、100°　　　　D、50°或65°

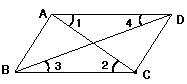
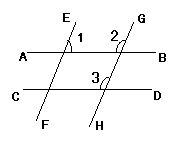
3、图1，在下列四组条件中，能判定AB∥CD的是　（　　）

（图1）

A、∠1=∠2　B、∠3=∠4 C、∠BAD+∠ABC=180°　D、∠ABD=∠BDC

4、下面的图形中，不是轴对称图形的是（　　 ）

A、有两个角相等的三角形；

B、有一个内角是40°，另一个内角是100°的三角形；

C、三个内角的度数比是2:3:4的三角形；

D、三个内角的度数比是1:1:2的三角形。

5、一些小立方块堆成的几何体，如下图，则其主视图为 （　　 ）

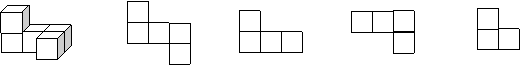　　　　　　　　 A、　　　　　　 B、　　　　　　 C、　　　　　　　 D、

6、已知一个三角形一边上的中线等于这边长的一半，那么这个三角形必定是（　　 ）　　

A、直角三角形　B、等腰三角形　 C、等腰直角三角形　 D、等边三角形

年龄	13	14	15	25	28	30	35	其他
人数	30	533	17	12	20	9	2	3

7、在对某社会机构的调查中收集到以下数据，你认为最能够反映该机构年龄特征的统计量是（　　 ）

A、平均数　　B、众数　　 C、方差　　D、标准差

（图2）

8、图2，在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B，在AB间建一条直水管，则水管的长为（　 ）

A、45m  　　B、40m　　 　C、50m　　 D、56m

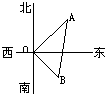9、直角三角形两条直角边的长分别为8和6，则斜边上的高为（　　）

A、2.4　　　B、4.8　　　 C、1.2　　 D、10

10、图3，边长为1的立方体中，一只蚂蚁从A顶点出发沿着立方体的外表面爬到B顶点的最短路程是（　　）．

（图3）

A、3　　　　B、　　　 C、2　　　 D、1

二、填空题（30）

11、图4是著名的上海“金茂大厦”，据你观察，

它更接近于何种几何体？　　　　　　　　　

（图5）

12、图5，AB∥CD，∠1+∠3=180°，试说明：EF∥GH

解：∵　　 　　　　　 （已知），

（图4）

∴∠2=∠3　( 理由：　　　　　　　　　　　　  )

（图6）

∵∠1+∠3=180°（已知）

　　　　　　　  ∴ 　　　　　　　 （等量代换）

∴EF∥GH　（理由: 　　　　　　　　　　　　　　　　）

13、一地图上两条笔直的公路如图6所示，比例尺为1：，则这两条公路之间的实际距离是　　　　　　　　　  km

14、在DABC中，AB=AC，ÐA=60°，则ÐB=_____　____，DABC是__　　_____三角形

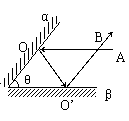
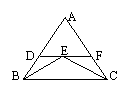15、在DABC中，如图7，AB=AC，ÐA=36°，BD平分ÐABC，则图中共有______个等腰三角形；他们分别是__________________________________________.

			（图8）		（图9）
	（图7）

16如图8，在DABC中，已知∠B和∠C的平分线交于点F，过点F作DE∥BC，交AB于点D，交AC于点E，若BD+CE=9，则线段DE的长为　　　　　　　　 

17、如图9放置的两平面镜α,β的夹角为θ，入射光线AO平行与β入射到α上，经过两次反射后的出射光线O’B平行于α，则交θ=　　　　　  °

17、有六根细木棒，它们的长分别是2，4，6，8，10，12（单位：cm），首尾连结能搭成直角三角形的三根细木棒分别是　　　　　　　  　　　　　；

18、一个印有“神六发射成功”字样的立方体纸盒表面展开图如图所示，则与印有“六”字面相对的表面上印有　　　　 字

19、为了预防“禽流感”的传播，检疫人员对某养殖场的家禽进行检验，任意抽取了其中的100只，此种方式属　　　　  调查，样本是　　　　　　　　　　　　　  ，样本容量是　　　　

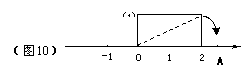20、如图10作一个长方形，以数轴的原点为旋转中心，将过原点的对角线顺时针旋转，使对角线的另一端点落在数轴正半轴的点A处，则点A表示的数是 　　　　　 ；这种研究和解决问题的方式，体现了　　　　的数学思想方法。（将符合的选项序号填在横线上）

 A、数形结合　 B、代入　　C、换元　　D、归纳

三、解答题（40）

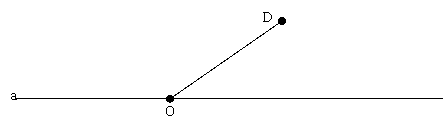
21、如图11，线段OD的一个端点O在直线a上，以OD为一边画等腰三角形，并且使另一个顶点在直线a上，这样的等腰三角形能画多少个?(并用直尺与圆规找出相应的等腰三角形)

	（图11）

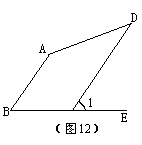
22、如图12，AB∥CD，∠B=61⁰，∠D=，求∠1和∠A的度数（写出过程）

24、某瓜农采用大棚栽培技术种植了一亩地的良种西瓜，这亩地产西瓜600个，在西瓜上市前该瓜农随机摘下了10个成熟的西瓜，称重如下：

西瓜质量(单位：千克)	5.4	5.3	5.0	4.8	4.4	4.0
西瓜数量(单位：个)	1	2	3	2	1	1

①这10个西瓜质量的众数和中位数分别是　　　和　　　　；

②计算这10个西瓜的平均质量，并根据计算结果估计这亩地共可收获西瓜约多少千克？（6分）

23、如图13，AC⊥BC，AD⊥BD，AD=BC，那么请你判断阴影部分图形的形状。

	（图13）

25、“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过70千米/小时，如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路面对车速检测仪正前方30米处，过了2秒后，测得小汽车与车速检测仪间距离为50米，这辆小汽车超速了吗？

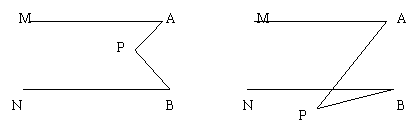
26、已知，如图，直线MA∥NB，

（1）若点P在直线MA与NB之间，你能得到∠APB=∠MAP+∠NBP这个结论吗？并说明你的理由。

（2）又若点P在两条直线MA与NB之外时，又会有什么结论？你还能就本题作出什么新的猜想。