八年级数学上期中测试模拟卷
一、选择题:
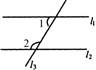 1、已知:如图,l1∥l2,∠1=50°, 则∠2的度数是( )
1、已知:如图,l1∥l2,∠1=50°, 则∠2的度数是( )
A.135° B.130° C.50° D.40°
2、 右边几何体的主视图是( ).
右边几何体的主视图是( ).

3、数据0、1、2、3、x的平均数是2,则这组数据的标准差是 ( )
![]()
![]() A、2 B、
C、10 D、
A、2 B、
C、10 D、
4、如果一个等腰三角形的一个角为120º,则这个三角形的顶角为( )
A、120º B、30º C、120º或30º D、90º
5、如图,∠ACB=Rt∠,D为AB的中点,已知AB=4,则CD的长为( )
A、8 B、4 C、2 D、1
6、有六根细木棒,它们的长分别是2,4,6,8,10,12(单位:cm),首尾连结能搭成直角三角形的三根细木棒分别是________.
A、2、4、6 B、4、6、8 C、6、8、10 D、 8、10、12
7、一架飞机向北飞行,两次改变方向后,前进的方向与原来的航行方向平行,已知第一次向左拐50°,那么第二次向右拐( )
A、40° B、50° C、130° D、150°
8、18.为了发展农业经济,致富奔小康,养鸡专业户王大伯2004
年养了2000只鸡,上市前,他随机抽取了10只鸡,称得重量
 统计如下表:估计这批鸡的总重量为( )kg
统计如下表:估计这批鸡的总重量为( )kg
| 重量(单位:kg) | 2 | 2.2 | 2.5 | 2.8 | 3 |
| 数量(单位:只) | 1 | 2 | 4 | 2 | 1 |
A、 5000 B、 4960 C、5600 D、无法确定
9、如图,CD是![]() 斜边AB上的高,将
斜边AB上的高,将![]() BCD沿CD折叠,B点恰好落在AB的中点E处,则
BCD沿CD折叠,B点恰好落在AB的中点E处,则![]() A等于( )
A等于( )
10、三角形两边的长分别是8和6,第三边的长是一元二次方程
![]() 的一个实数根,则该三角形的面积是( )
的一个实数根,则该三角形的面积是( )
A、 24 B、 24或![]() C、48 D、
C、48 D、![]()
二、填空题:
11、在数据1,2,3,1,2,2,4中,众数是
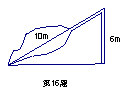
12、如图,受今年的强台风“韦帕”的影响,张大爷家屋前9m远处有一棵大树。从离地面6m处折断倒下,量得倒下部分的长是10m,大树倒下时会砸到张大爷的房子吗?
答: (“会”和“不会”请选填一个)

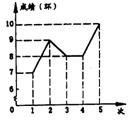
13、如图是小敏五次射击成绩的图,根据图示信息,则此五次成绩的平均数是________环。
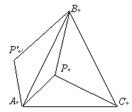
14、.一位美术老师在课堂上进行立体模型素描教学时,把14个棱长为1分米的正方体摆在课桌上成如图6形式,然后他把露出的表面都涂上不同的颜色,则被他涂上颜色部分的面积为 平方分米.
15、如图,P是正三角形 ABC 内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P'AB ,则点P与点P' 之间的距离为_______,∠APB=______
16、自然数中有许多奇妙而有趣的现象,很多秘密等待着我们去探索!比如:对任意一个自然数,先将其各位数字求和,再将其和乘以3后加上1,多次重复这种操作运算,运算结果最终会得到一个固定不变的数R,它会掉入一个数字“陷井”,永远也别想逃出来,没有一个自然数能逃出它的“魔掌”。那么最终掉入“陷井”的这个固定不变的数R=_____。
三、解答题
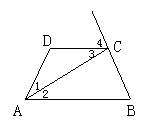 17、如图,已知∠4=∠B,∠1=∠3,求证:AC平分∠BAD
17、如图,已知∠4=∠B,∠1=∠3,求证:AC平分∠BAD
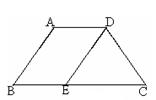 18、(本小题8分)如图,在梯形ABCD中,AD∥BC,AB=DC,∠B=60º,DE∥AB。
18、(本小题8分)如图,在梯形ABCD中,AD∥BC,AB=DC,∠B=60º,DE∥AB。
求证:(1)DE=DC;
(2)△DEC是等边三角形。
19、、某企业生产部共有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人,某月加工零件的个数:
| 每人加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
| 人 数 | 1 | 1 | 2 | 6 | 3 | 2 |
⑴写出这15人该月加工零件的平均数、中位数和众数;
⑵假如生产部负责人把每位工人的月加工零件个数定为260件,你认为这个定额是否合理? 为什么?
|
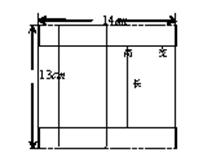
20、扬子江药业集团生产的某种药品包装盒的侧面展开图如图所示.如果长方体盒子的长比宽多4![]() ,求这种药品包装盒的体积.
,求这种药品包装盒的体积.
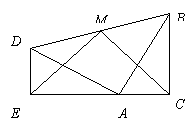 21、两个全等的含30°,60°角的三角板ADE和ABC,E、A、C在一条直线上,连结BD,取BD的中点M,连结ME,MC,试判断△EMC的形状,并说明理由.
21、两个全等的含30°,60°角的三角板ADE和ABC,E、A、C在一条直线上,连结BD,取BD的中点M,连结ME,MC,试判断△EMC的形状,并说明理由.
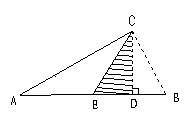
22、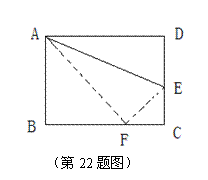 (本题9分)如图,折叠矩形的一边AD,使得点D落在BC边上的点F处,已知AB=8cm, BC=10cm,则EC的长是多少?
(本题9分)如图,折叠矩形的一边AD,使得点D落在BC边上的点F处,已知AB=8cm, BC=10cm,则EC的长是多少?
23、我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等,那么在什么情况下,它们会全等?
(1) 阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等。
对于这两个三角形均为钝角三角形,可证明它们全等(证明略)
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
已知:△ABC、△![]() 均为锐角三角形,AB=
均为锐角三角形,AB=![]() ,BC=
,BC=![]() ,∠C=∠
,∠C=∠![]() ,证明:△ABC≌△
,证明:△ABC≌△![]() (请你将下列证明过程补充完整)
(请你将下列证明过程补充完整)
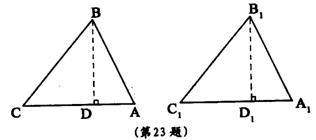
证明:分别过点B、![]() ,作BD⊥CA于D,
,作BD⊥CA于D,![]() 于
于![]() ,
,
则∠BDC=![]() =90º,∵BC=
=90º,∵BC=![]() ,∠C=∠
,∠C=∠![]()
∴△BCD≌△![]() ∴BD=
∴BD=![]()
(2) 归纳与叙述:由(1)可得到一个正确结论,请你写出这个结论。
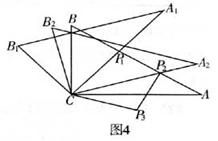
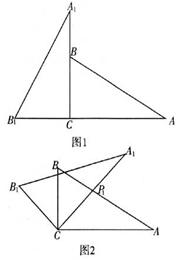
24、将两块含30°角且大小相同的直角三角板如图1摆放。
(1)将图1中△![]() 绕点C顺时针旋转45°得图2,
绕点C顺时针旋转45°得图2,
点![]() 与AB的交点,若AP1=2,求CP1的长。
与AB的交点,若AP1=2,求CP1的长。
(2)将图2中△![]() 绕点C顺时针旋转30°到△
绕点C顺时针旋转30°到△![]() (如图3),点
(如图3),点![]() 与AB的交点。线段
与AB的交点。线段![]() 之间存在一个确定的等量关系,请说明:
之间存在一个确定的等量关系,请说明:![]() 理由;
理由;
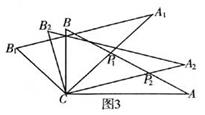 (3)将图3中线段
(3)将图3中线段![]() 绕点C顺时针旋转60°到
绕点C顺时针旋转60°到![]() (如图4),连结
(如图4),连结![]() ,请说明:
,请说明:![]() ⊥AB.
⊥AB.