《一次函数》测试题
姓名______学号_______
一、细心填一填（每题3分，共30分）
1、已知一个正比例函数的图象经过点（-2，4），则这个正比例函数的表达式是 。
2、若函数y= -2xm+2是正比例函数，则m的值是 。
3、已知一次函数y=kx+5的图象经过点（-1，2），则k= 。
4、已知y与x成正比例，且当x＝1时，y＝2，则当x=3时，y=____ 。
5、点P（a，b）在第二象限，则直线y=ax+b不经过第 象限。
6、已知一次函数y=kx-k+4的图象与y轴的交点坐标是(0，-2)，那么这个一次函数的表达式是______________。
7、已知点A(-
，a), B(3，b)在函数y=-3x+4的象上,则a与b的大小关系是____ 。
8、地面气温是20℃,如果每升高100m,气温下降6℃,则气温t（℃）与高度h（m）的函数关系式是__________。
9、一次函数y=kx+b与y=2x+1平行,且经过点(-3,4),则表达式为： 。
10、写出同时具备下列两个条件的一次函数表达式（写出一个即可） 。
（1）y随着x的增大而减小， （2）图象经过点（1，-3）。
二、精心选一选（每题3分，共24分）
11、下列函数（1）y=πx (2)y=2x-1 (3)y= (4)y=2-1-3x (5)y=x2-1中，是一次函数的有（ ）
（A）4个 （B）3个 （C）2个 （D）1个
12、下面哪个点不在函数
的图像上（ ）
（A）（-5，13） （B）（0.5，2） （C）（3，0） （D）（1，1）
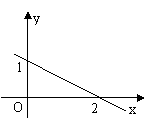
13、直线y=kx+b在坐标系中的位置如图，则( ) （第13题图）
（A）
（B）
（C）
（D）
14、下列一次函数中，
随着
增大而减小而的是 （ ）
（A）
（B）
（C）
（D）
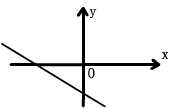15、已知一次函数y=kx+b的图象如图所示，则k，b的符号是( )
(A) k>0，b>0 (B) k>0，b<0
(C) k<0，b>0 (D) k<0，b<0
（第15题图）
16、函数y=(m+1)x-(4m-3)的图象在第一、二、四象限，那么m的取值范围是( )
（A）
（B）
（C）
（D）
17、一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h (厘米)与燃烧时间t (时)的函数关系的图象是( )
 |
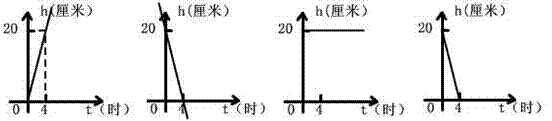(A) (B) （C） （D）
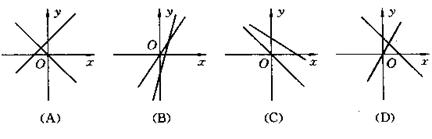
18、下图中表示一次函数y＝mx+n与正比例函数y＝m nx(m ，n是常数，且mn
0)图像的是( )．
三、耐心做一做(第19~23题，每题6分，第24、25题，每题8分，共46分)
19、已知一个正比例函数和一个一次函数的图象相交于点A(1，4)，且一次函数的图象与x轴交于点B(3，0)
(1)求这两个函数的解析式；
(2)画出它们的图象；
20、已知y -2与x成正比，且当x=1时，y= -6
(1)求y与x之间的函数关系式 (2)若点(a，2)在这个函数图象上，求a的值
21、已知一次函数y=kx+b的图象经过点(-1， -5)，且与正比例函数y= x的图象相交于点(2，a)，求
(1)a的值
(2)k，b的值
(3)这两个函数图象与x轴所围成的三角形的面积。
22、某市自来水公司为限制单位用水，每月只给某单位计划内用水3000吨，计划内用水每吨收费1.8元，超计划部分每吨按2.0元收费。
（1）写出该单位水费y（元）与每月用水量x（吨）之间的函数关系式：_________________
①当用水量小于等于3000吨 ；②当用水量大于3000吨 。
（2）某月该单位用水3200吨，水费是 元；若用水2800吨，水费 元。
（3）若某月该单位缴纳水费9400元，则该单位用水多少吨？
23、已知函数y=(2m+1)x+m -3
(1)若函数图象经过原点，求m的值
(2)若这个函数是一次函数，且y随着x的增大而减小，求m的取值范围。
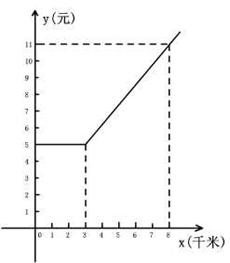24、如图是某市出租车单程收费y (元)与行驶路程x (千米)之间的函数关系图象，根据图象回答下列问题：
(1)当行使路程为8千米时，收费应为 元；
(2)从图象上你能获得哪些信息?(请写出2条)
①
②
(3)求出收费y (元)与行使路程x (千米) (x≥3)之间的函数关系式。
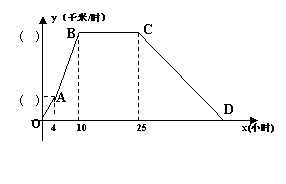
25、某气象研究中心观测一场沙尘暴从发生到结束全过程，开始时风暴平均每小时增加2千米/时，4小时后，沙尘暴经过开阔荒漠地，风速变为平均每小时增加4千米/时，一段时间，风暴保持不变，当沙尘暴遇到绿色植被区时，其风速平均每小时减小1千米/时，最终停止。 结合风速与时间的图像，回答下列问题：
（1）在y轴（ ）内填入相应的数值；
（2）沙尘暴从发生到结束，共经过多少小时？
（3）求出当x≥25时，风速y（千米/时）与时间x（小时）之间的函数关系式。
（4）若风速达到或超过20千米/时，称为强沙尘暴，则强沙尘暴持续多长时间？
 |
【参考答案】
一、1、y=-2x,2、-1,3、3,4、6,5、三，6、y=6x-2,7、a＞b,8、t=-0.06h+20,9、y=2x+10,
10、y=-3x或y=-2x-1等,11、B,12、C,13、B,14、D,15、D,16、C,17、D,18、C,19(1).y=4x,y=x+3,(2)图略.20(1).y=-8x+2,(2).a=0,21(1).a=1,(2).k=2,b=-3,(3).3/4
22(1).①y=1.8x,②y=2x-600,(2).5800,5040,(3).5000,23(1).m=3,(2).m＜-1/2,
24(1).11,(2).①出租车的起步价是5元，②出租车起步价的路程范围是3公里之内（包括3公里），（3）.y=1.2x+1.4(x≥3),25(1).8,32,(2).57,(3).y=-x+57(x≥25),(4).30.