第十一章 《一次函数》检测试卷
班级________姓名________座号________
一、填空题（每题3分，共30分）
1．在圆的周长公式C=2πr中，变量是________，常量是_________.
2．函数
中自变量x的取值范围是___________.
3．将直线y＝3x向下平移5个单位，得到直线的解析式是
4．正比例函数
，当m
时，y随x的增大而增大.
5．若函数
图象经过点（1，2），则m=
.
6．直线
与x轴交点的坐标是________,
7．平行四边形相邻的两边长为x、y，周长是30，则y与x的函数关
系式是__________．
8．已知函数y=2x—4，当 
时，函数图象在第四象限.
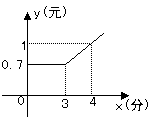
9．在某公用电话亭打电话时，需付电话费y（元）
与通话时间 x（分钟）之间的函数关系用图象表示
如图.小明打了2分钟需付费______元；小莉打了
4分钟需 付费_______ 元.
10．王华和线强同学在合作电学实验时，记录下电流I（安 培）与电阻R（欧）有如下对应关系.观察下表：
| R | …… | 2 | 4 | 8 | 10 | 16 | …… |
| I | …… | 16 | 8 | 4 | 3.2 | 2 | …… |
你认为I与R间的函数关系式为________；当电阻R＝5欧时，电流
I＝_______安培.
二、选择题 （每题3分，共21分）
1．下列各图给出了变量y与x之间的函数是 （ ）
2.下列给出的四个点中，不在直线y=2x-3上的是 （ ）
A.（1， -1） B.（0， -3） C.（2， 1） D.（-1，5）
3.若
是正比例函数，则b的值是 （ ）
A.0 B.
C.
D.
4.关于函数
，下列结论正确的是
（ ）
A．图象必经过点（﹣2，1） B．图象经过第一、二、三象限
C．当
时，
D．
随
的增大而增大
5.已知点（-4，y1），（2，y2）都在直线y= - x+2上，则y1 ,y2大小关
系是 ( )
A． y1 > y2 B． y1 = y2 C．y1 < y2 D． 不能比较
6.汽车由Ａ地驶往相距120km的B地，它的平均速度是30km/h，则汽车距Ｂ地路程s(km)与行驶时间t(h)的函数关系式及自变量t的取值范围是（ ）
Ａ．S=120－30t (0≤t≤4) Ｂ．S=120－30t (t>0)
Ｃ．S=30t (0≤t≤40) Ｄ．S=30t (t<4)
7.小明的父亲饭后散步，从家中走20分钟到一个离家900米的报亭看10分钟的报纸后，用15分钟返回家中，下列图形中表示小明父亲离家的时间与距离之间的关系是（ ）
 |
A B C D
三、解答题(共49分)
1．（6分）甲市到乙市的包裹邮资为每千克0.9元，每件另加手续费0.2元.求总邮资y（元）与包裹重量x（千克）之间的函数解析式，并计算5千克重的包裹的邮资．
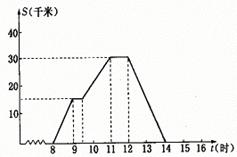
2．（6分）一天上午8时，小华去县城购物，
到下午2时返回家，结合图象回答：
(1)小华何时第一次休息？
(2)小华离家最远的距离时多少？
(3)返回时平均速度是多少？
3.（6分）在同一坐标系内画出一次函数y1=-x+1 与y2=2x-2的图象， 并根据图象回答下列问题：
（1）直接写出，当x取何值时y1 =y2
（2）直接写出，当x取何值时y1 ＜y2
4．（6分）已知直线
经过点（1，2）和点（
，4），求这条直线的解析式.
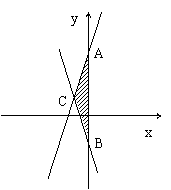5．（8分）如图示：已知直线y=2x+3与直线y=-2x-1.
（1） 写出两直线与y轴交点A，B的坐标;
（2） 求两直线交点C的坐标;
（3） 求△ABC的面积.
6．（8分）某影碟出租店开设两种租碟方式：一种是零星租碟，每张收费1元，另种是会员卡租碟，办卡费每月12元，租碟费每张0.4元，小彬经常来店租碟，若每月租碟数量是x张。
（1） 写出零星租碟方式应金额 y1（元）与租碟张数x（张）之间的函数关系式；
（2） 写出会员卡租碟方式应金额 y2（元）与租碟张数x（张）之间的函数关系式；
（3）小彬选哪种租碟方式更合算？
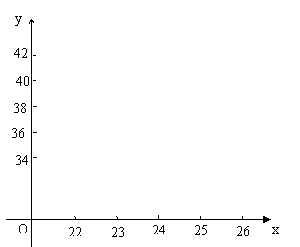
7．（9分）爱动脑筋的小明同学在买一双新的运动鞋时，发现了一些有趣现象，即鞋子的号码与鞋子的长（cm）之间存在着某种联系，经过收集数据，得到下表：
| 鞋长x（cm） | … | 22 | 23 | 24 | 25 | 26 | … |
| 码数y | … | 34 | 36 | 38 | 40 | 42 | … |
请你代替小明解决下列问题：
（1） 根据表中数据，在同一直角坐标系中描出相应的点，你发现这些点在哪
一种图形上？
（2）猜想y与x之间满足怎样的函数关系式，并求出 y与x之间的函数关系式，验证这些点的坐标是否满足函数关系式.
（3）当鞋码是30码时，鞋长是多长？