八年级数学上学期期中测试卷
班级 姓名 座号 评分
一、选择题:（每小题3分 共30分）
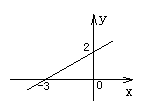
1、一次函数
的图象经过（ ）
（A）第一、三、四象限 （B）第二、三、四象限
（C）第一、二、三象限 （D）第一、二、四象限
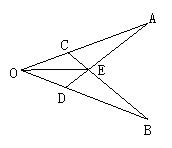
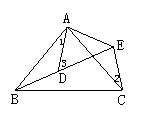
2、如图1所示，已知OA=OB，OC=OD，AD，BC相交于E，则图中全等的三角形的个数是（ ）．
A．2 B．3 C．4 D．5
(1) (2) (3)
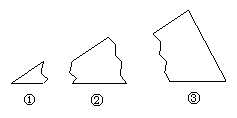
3、如图2所示，某同学将一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（ ）．
A．带①去 B．带②去 C．带③去 D．带①②去
4、如图3，△ABC≌△BAD，A和B，C和D是对应顶点，如果AB=6cm，BD=5cm，AD=4cm，那么BC的长是（ ）．
A．4cm B．5cm C．6cm D．无法确定
5、已知点（-2，y1），（-1，y2），（1，y3）都在直线y=
-
x+b上，则y1，y2，y3的值的大小关系是（ ）．
A．y1>y2>y3 B．y1<y2<y3 C．y3>y1>y2 D．y3>y1>y2
6、一天，王老师从学校坐车去开会，由于途中塞车，他只好步行赶到会场，开完会后，他直接回到学校，下图中能体现他离学校的距离y（千米）与时间x（时）的关系的图象是（ ）
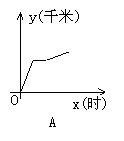
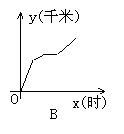
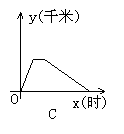
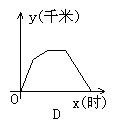
7、下列条件：①AB=A′B′，BC=B′C′，AC=A′C′；②∠A=∠A′，∠B=∠B′，∠C=∠C′；③AB=A′B′，BC=B′C′，∠C=∠C′；④AB=A′B′，∠B=∠B′，∠C=∠C′其中不能说明△ABC和△A′B′C′全等的有（ ）
A．1个 B．2个 C．3个 D．4个
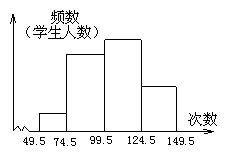
8、体育委员统计了全班同学60秒跳绳的次数，并列出下面的频数分布表：
| 次数 （ |
|
|
|
|
|
|
|
| 频数 （人数） | 2 | 4 | 21 | 13 | 8 | 4 | 1 |
）
从表中可知，组距和组数分别是（ ）
（A）组距8，组数20; （B）组距20，组数7;
（C）组距7，组数20; （D）组距40，组数7;
9、在某扇形统计图中，其中某一部分扇形面积所对的圆心角是
，那么它所代表的部分占总体的（ ）
（A）
（B）
（C）
（D）
10、右图中两条直线
和
和交点坐标
可以看作下列方程组中（ ）的解。
（A）
（B）
（C）
（D）
二、填空题（每小题4分，共24分）
1、函数y=
中自变量x的取值范围是___________．
2、函数y=kx+b（k≠0）的图象平行于直线y=2x+3，且交y轴于点（0，-1），则其解析式是_________．
3、若一次函数y=3x+b经过点A（1，7），该函数图像经过点B（4，______）和点C（_____，0）
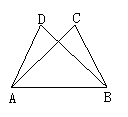
4、如图4所示，∠B=∠D=90°，要证明△ABC与△ADC全等，还需要补充的条件是________．
(4) (5) (6)
5、如图5所示，AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=_____．
6、函数y=kx+b的图像如图6所示，则当y<0时，x的取值范围是________．
三、解答题（共46分）
1、（8分）观察下列大棚蔬菜种植情况统计图，回答问题：
⑴填上扇形统计图中括号中的数据；
⑵哪种蔬菜种植面积最大？
⑶哪两种蔬菜种植面积较接近？
(4)已知豆角种了27公顷，种植蔬菜的总面
积是多少公顷？种植西红柿多少公顷？
2、（8分）为了了解某校八年级男生的体能情况，从该校八年级抽取50名男生进行1分钟跳绳测试，把所得数据整理后，画出频数分布直方图（如图）．已知图中从左到右第一、第二、第三、第四小组的频数的比为1：3：4：2．（1）求第二小组的频数和频率；（2）求所抽取的50名男生中，1分钟跳绳次数在100次以上（含100次）的人数占所抽取的男生人数的百分比．
3、（8分）如图，AB=CD，AE⊥BC，DF⊥BC，CE=BF。求证：AE=DF
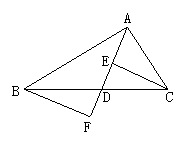
4、（10分）如图，AD是△ABC的中线，CE⊥AD于E，BF⊥AD交AD的延长线于F，求证：CE=BF。
5、（12分）如图，直线y=kx + 6与X轴Y轴分别交于点E、F，点E的坐标为（-8，0）点A的坐标为（-6，0）。
（1）求K的值。
（2）若点P（X，Y）是第二象限内的直线的一个动点，当点P运动过程中，试写出
OPA的面积S与X的函数关系式，并写出自变量X的取值范围。
（3）当P运动到什么位置时，
OPA的面积为 
。