八年级数学第一学期阶段性检测试题卷
出卷人: 丁新宇 审核人: 黄瑛珠 王庆丽 周云霞
考生须知：
1． 本试卷分试题卷和答题卷两部分。满分120分，考试时间100分钟。
2．
答题时，必须在答题卷密封区内写明校区、考场、座位号、姓名、班级等内容。答题必须书写在各规定区域之内，超出答题区域的答案将被视为无效。
一、选择题（每题3分，共30分）
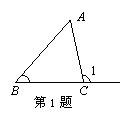
1．如图，∠B与∠1是（ ）
A．对顶角 B．同位角 C．内错角 D．同旁内角
2．下列说法最恰当的是（ ）
A.某工厂质检人员检测灯泡的使用寿命采用普查法
B.防治某突发性传染病期间，某学校对学生测量体温，应采用抽样调查法
C.要了解某小组各学生某次数学测试成绩采用抽样调查法
D.了解我市中学生的身体素质状况采用抽样调查法
3．如图是一块带有圆形空洞和方形空洞的小木板，则下列物体中既可以堵住圆形空洞，又可以堵住方形空洞的是（ ）
4．如图，由AB∥CD，可以得到（ ）
A．∠1=∠2 B．∠2=∠3
C．∠1=∠4 D．∠3=∠4
5．一个正方体的每个面都写有一个汉字，其平面展开图如图所示，那么在该正方体中，和“试”相对的字是（ ）
A．祝 B．你 C．考 D．功
7.下列条件中，不能判定两个直角三角形全等的是 （ ）
A.两个锐角对应相等 B.一条直角边和一个锐角对应相等
C.两条直角边对应相等 D.一条直角边和一条斜边对应相等
6.调查表明，2006年杭州市城镇家庭年收入在3万元以上的家庭户数低于40％. 据此判断，下列说法正确的是( )
A. 家庭年收入的众数一定不高于3万
B. 家庭年收入的中位数一定不高于3万
C. 家庭年收入的平均数一定不高于3万
D. 家庭年收入的平均数和众数一定都不高于3万
8.如图，△ABC中，∠C=90°，AB的中垂线DE交AB于E，
交BC于D，若AB=10，AC=6，则△ACD的周长为（ ）
A.16 B.14 C.20 D.18
9．将一条两边沿平行的纸带如图折叠，若∠1＝62º，则∠2等于（ ）
A. 62º B.56º C.45º D. 30º
10.如图，Rt△ABC中，CF是斜边AB上的高，角平分线BD交CF于G，DE⊥AB于E，则下列结论①∠A=∠BCF , ② CD=CG=DE, ③AD=BD , ④ BC=BE中正确的个数是（ ）
A.1 B.2 C.3 D.4
二、填空题（每题3分，共30分）
11．等腰三角形的两边长分别是4厘米和9厘米，则周长为 厘米.
12．如图，∠1＋∠2＝180°，∠3＝108°，则∠4＝ °.
13.下表是丁老师家9月份连续 8天每天中午电表的读数：
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 电表读数（千瓦·时） | 25 | 29 | 32 | 37 | 43 | 50 | 56 | 60 |
请你估计丁老师家9月份（30天）的用电量是 千瓦·时。
14.如图，AB∥CD，∠2＝70º，则∠1 + ∠2 + ∠3的度数为 .
15．直角三角形斜边上的高与中线分别是5cm和6cm，则它的面积是 cm2.
16．一个底面为正方形的直棱柱侧面展开图是边长为8的正方形，则它的表面积为 .
17.如图,在等腰
中, 
,
,BE是AC边上的高,则
= º.
18.如图所示，电视台的摄像机1、2、3、4在不同位置拍摄了四幅画面，则A、B图象分别是______号摄像机所拍。
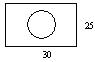
19．如图是一个长方形零件示意图，根据图中的数据（单位：mm），则两孔中心A和B之间的距离为 .
20.如图，在等边
中，
，点
在
上，且
，点
是
上一动点，连结
，作
，使
，要使点
恰好落在
上，则
的长是 .
三、解答题（共60分）
21．（ 8分）在如图所示的网格中，每个小正方形的边长均为1个单位。
（1）请你在左图中画出两条平行线，要求每条直线至少经过两个格点（网格的交点），但是又不与网格线重合；
（2）请你在右图中画一个以格点为顶点，面积为10个平方单位的等腰三角形。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
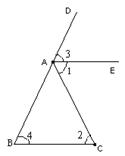22.（8分）如图，
是的一个外角，
平分，且
，那么
吗？为什么？
23．（8分）如图所示是一个几何体的三视图。
（1）说明组成该几何体的两部分分别是什么几何体？
（2）求该几何体的体积（
取3.14，长度单位cm）；
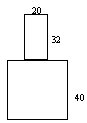
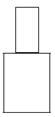
主视图 左视图 俯视图
24．（8分）某学校举行演讲比赛，选出了10名同学担任评委，并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分（满分为10分）：
方案1 所有评委所给分的平均数．
方案2 在所有评委所给分中，去掉一个最高分和一个最低分，再计算其余给分的平均数．
方案3 所有评委所给分的中位数．
方案4 所有评委所给分的众数．
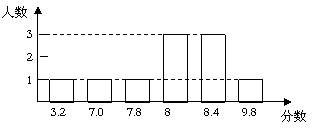为了探究上述方案的合理性，先对某个同学的演讲成绩进行了统计实验．下面是这个同学的得分统计图：
（1）分别按上述4个方案计算这个同学演讲的最后得分；
（2）根据（1）中的结果，请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分．
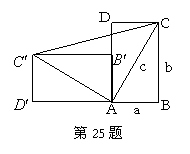25.（8分）一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的证明方法.
如图，火柴盒的一个侧面
（是一个长方形）倒下到
的位置，连结
，设
.
（1） 试用
有关的代数式表示梯形
的面积;
（2） 试用
有关的代数式分别表示△ABC、△
、△
的面积；
（3）由（1）和（2）的结论证明勾股定理：
。
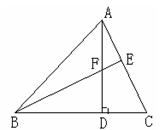
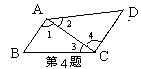
26. (10分)如图，AD为△ABC的高，E为AC上一点，BE交AD于F，且有BF=AC,FD=CD。
（1）请说明△BFD≌△ACD；
（2）判断BE与AC的位置关系，并说明理由。
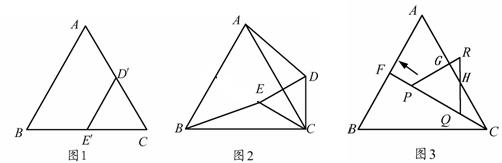
27．（10分）如图1，是边长分别为4和3的两个等边三角形纸片ABC和CDˊEˊ叠放在一起．
（1）（6分）操作：固定△ABC，将△CDˊEˊ绕点C顺时针旋转得到△CDE，连结AD、BE，如图2．探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论；
（2）（2分）操作：固定△ABC，若将△CDˊEˊ绕点C顺时针旋转30°得到△CDE，连结AD、BE，CE的延长线交AB于点F，在线段CF上沿着CF方向以每秒1个单位长的速度平移，平移后的△CDE设为△PQR，如图3．
探究：在图3中，除三角形ABC和CDE外，还有哪个三角形是等腰三角形？写出你的结论（不必说明理由）；
（3）（2分）探究：如图3，在（2）的条件下，设△PQR移动的时间为x秒，△PQR与△AFC重叠部分的面积为y，写出用x表示y的关系式为y= 。
