八年级数学第一学期期中独立作业
（命题人：金弘鑫）
考前寄语：同学们，请仔细审题，认真做答！
一、选择题（每小题3分，共30分）
1.如图，两只手的食指和拇指在同一个平面内，它们构成的一对角可看成是（ ）
A.内错角 B.同位角
|
2.如图，若AB∥CD，则有①∠A＋∠B＝180º，②∠B＋∠C
＝180º，③∠C＋∠D＝180º．上述结论正确的是（ ）
A.只有① B.只有② C.只有③ D.只有①和③
3.如果一个等腰三角形的一个角为30º，则这个三角形的顶角为……………（ ）
A.120º B.30º C.120º或30º D.90º
4. 若点P（m，n）是第二象限的点， 则点Q（m-1，n+2）是第( )象限的点。
A.第一象限 B.第二象限 C 第三象限 D.第四象限
5.下列调查方式，你认为正确的是………………………………………………（ ）
A.了解一批炮弹的杀伤半径，采用普查方式
B.调查你所在班级全体学生的身高，采用普查方式
C.要保证“神舟6号”载人飞船成功发射，对重要零部件采用抽查方式检查
D.了解金华市居民日平均用水量，采用普查方式
6.下列命题错误的是………………………………………………………………（ ）
A.等腰三角形两腰上的中线相等 B.等腰三角形两腰上的高相等
C.等腰三角形的中线与高互相重合
D.等腰三角形顶角平分线上任一点到底边两端点的距离相等
7. 下列四个图形中，可以是一个立方体表面展开图的是………………………（ ）
 |
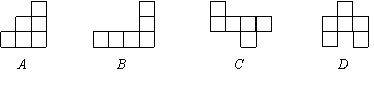8．八年级某班甲、乙两组各12名学生参加体育成绩(满分30分)经统计如下表，则列结论一定正确的是为……………………………………………………………………( )
| 组别 | 人数 | 平均分数 | 方差 | 中位数 | 众数 |
| 甲 | 12 | 23 | 46.0l | 24 | 22 |
| 乙 | 12 | 23 | 44.8l | 22 | 2l |
①甲、乙两组学生成绩平均水平相同；②乙组的成绩较稳定；
③甲组优秀率不小于乙组的优秀率(注：成绩大于等于24分为优秀)；
④甲组得22分的人数与乙组得21分的人数相间．
A．①②③④ B．①②③ c．①③ D．②④
9．某种肥皂原零售价每块3元，凡购买2块以上(包括2块)，商场推出两种优惠销售办法．第一种：一块肥皂按原价，其余按原价的七折销售；第二种：全部按原价的八折销售．你在购买相同数量肥皂的情况下，要使第一种方法比第二种方法得到的优惠多，最少需要买 ( )块肥皂．
A．4 B．5 C．6 D．7
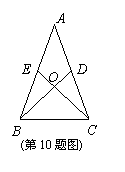
10.如图，在△ABC中，D、E分别是AC、AB上的点，BD与CE交于点O，
给出下列四个条件：①∠EBO＝∠DCO；②∠BEO＝∠CDO；③BE＝CD；
④OB＝OC，其中不能判定△ABC是等腰三角形的是……（ ）
A. ①和③ B. ②和④ C. ②
和③ D. ③和④
二、填空题（每题3分，共24分）
11.如图,
和
是直线AB、直线______被直线_______所截构成的________角.
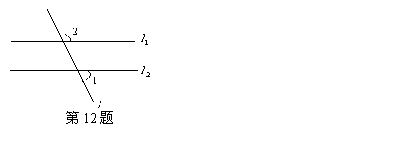12.如图,直线
,
被直线
所截,
,若
,则
_________.
 |
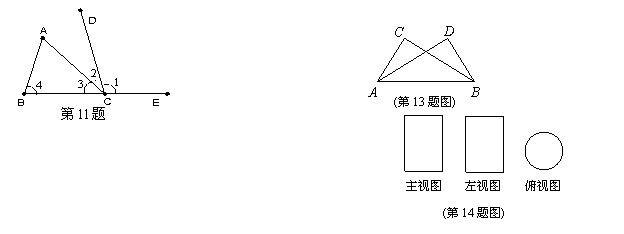13.如图，已知∠C＝∠D＝90º，请你添加一个适当的条件：
_____________,使△ACB≌△BDA．
14.某物体的三种视图如图所示，那么该物体的形状____________
15．小亮记录了他7天中每天完成家庭作业所需的时间，结果如下
(单位：分)80、70、 90、60、70、70、80，这组数据的中位数 ．
16.随即抽取某城市其中30天的空气质量状况如下表
| 污染指数(w) | 40 | 70 | 90 | 110 | 120 | 140 |
| 天数(f) | 3 | 5 | 10 | 7 | 4 | l |
其中w≤50时，空气质量为优；50<w≤100时，空气质量为良；l00<w≤150
时，空气质量为轻度污染．估计该城市一年365天空气质量达到良以上的约有 天．
17．已知P点在y轴上，到x轴的距离是2，则点P的坐标是 ___
18. 在直角坐标系中，已知点A（1，1），在
轴上确定点P，使△AOP为等腰三角形，则符合条件的点P的坐标为
___
三、计算题（共46分）
19.(5分）解不等式组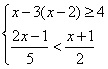
，并把解集在数轴上表示出来。
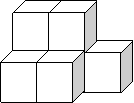
20.（5分）如图，图中的物体由7块相同的立方体组成，请画出它的三视图
 |
21.（6分）某市体校准备挑选一名跳高运动员参加全市中学生运动会，对跳高运动队的甲、乙两名运动员进行了8次选拔比赛，他们的成绩（单位：cm）如下：
甲：170 165 168 169 172 173 168 167
乙：161 173 174 164 163 172 170 175
（1）甲、乙两名运动员的跳高平均成绩分别是多少？
（2）哪名运动员的成绩更为稳定？为什么？
（3）若预测，跳过165cm就很可能获得冠军．该校为了获得冠军，可能选哪位运动员参赛？若预测跳过170cm才能得冠军呢？
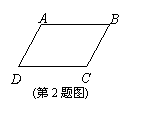
22.（6分）如图，AD是等腰三角形ABC的底边BC上的高，DE∥AB，交AC于点E，判断△ADE是不是等腰三角形，并说明理由.
23．（6分）阅读题：(先阅读再解答问题)
含有一个未知数，并且未知数的最高次指数是2的方程，叫做一元二次方程，如：x2一2x+l=O．已知关于x的一元二次方程a x2+bx+c=O(a、b、c：表示已知量，a≠0)的解的情况是：①当b2一4ac>0时，方程有两个不相等的解；
②当b2一4ac=0时，方程有两个相等的解(即一个解)；
③当b2一4ac<0时，方程没有解．
(1)一元二次方程2x2一4x+5=O有几个解?为什么?
(2)当a取何值时，关于x的一元二次方程x2一2x+(a一2)=0有两个不相等的解.
24．（8分）我市某房地产开发公司计划建造A、B两种户型的住房共80套，该公司所筹资金不少于2090万元，但不超过2096万元，且所筹资金全部用于建房，两种户型的建房和售价如下表
| A | B | |
| 成本(万元／套) | 25 | 28 |
| 售价(万元／套) | 30 | 34 |
(1)若该公司打算建A型房x套，则打算建B型房 套,所建房全售出后获得的总利润为 万元(用含X的代数式表示)；
(2)该公司对这两种户型有哪几种建房方案?哪种方案获得的利润最大?．
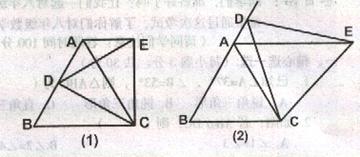
25．（10分）如图(1)，等边△ABC中，D是AB边上的动点，以CD为一边，向上作等边△EDC，
连结AE．
(1)△DBC和△EAC会全等吗?请说说你的理由．
(2)试说明AE∥BC的理由．
(3)如图(2)，将(1)中动点D运动到边BA的延长线上，所作△EDC仍为等边三角形，请问是否仍有AE∥BC?证明你的猜想．
兰六中2007学年第一学期八年级数学期中独立作业答案
一、选择题．(每小题3分，共30分)
l、A 2、B 3、C 4、B 5、B 6、C 7、C 8、B 9、A 10、D
二、填空题．(每小题3分，共24分)
11、CD BC 同位角 12、120 13、答案不唯一 14、圆柱体 15、70 16、219 17、（0，2）或（0，-2） 18、(一√2￣,0)或(√2￣,0)或（2，0）或（1，0）
三、解答题．(共66分)
19、-7<X≤1
20、略
2l、（1）略（2）甲（3）甲 乙
22、是 可证 AE=DE
23、(1)∵b2-4ac=(-4)2-4×2 × 5=-24<0．∴方程没有解
(2)由题意得：(一2)2一4×l×(a-2)>0 解得：a<3
∴当a<3时，方程有两个不相等的解
24、(1)80- X 480-X
(2)由题意得：2090≤25X+28(80-X)≤2096 解得48≤X≤50
∵X是整数 ∴X=48，49，50 即有三种建房方案：
A型48套，B型32套；A型49套，B型3l套；A型50套，B型30套
由W=480-X知，当X=48时，w最大。
即建A型48套，B型32套获得的利润最大．
25、(1)ADBC和AEAC会全等 证明对得3分
(2)∵△DBC≌△EAC ∠EAC=∠B=600 又∠ACB=600 ∴∠EAC=∠ACB
∴AE∥BC
(3)结论：AE∥BC
理由：∵△ABC、△EDC为等边三角形 ∴BC=AC，DC=CE，∠BCA=∠DCE=600
∠BCA+∠ACD=∠DCE+∠ACD 即∠BCD=∠ACE 在ADBC和AEAC中，BC=AC
∠BCD=∠ACE CD=CE ∴△DBC≌△EAC(SAS)．∴∠EAC=∠B=600又∠ACB=600．
∴∠EAC=∠ACB ∴AE∥BC