数学《不等式与不等式组》单元检测（满分：150分）
姓名： 得分：
一、选择题（每小题４分，共40分）
1． 若m＞n，则下列不等式中成立的是（ ）
A．m + a＜n + b B．ma＜nb C．ma2＞na2 D．a－m＜a－n
2．不等式4（x
2）＞2（3x + 5）的非负整数解的个数为( )
A．0个 B．1个 C．2个 D．3个
3．若不等式组的解集为1≤x≤3，则图中表示正确的是（ ）
A． B． C． D．
4．若方程
的解是负数，则
的取值范围是（ ）
A．
B． 
C． 
D．
5．不等式
的解集为
，则 的值为（ ）
A．4 B．2 C．
D． 
6．不等式组
的解集是（
）
A．
≥
1 B．＜5 C．1≤＜5 D．≤1或＜5
7．在
ABC中，AB=14，BC=2x，AC=3x，则x的取值范围是（ ）
A、x＞2.8 B、2.8＜x＜14 C、x＜14 D、7＜x＜14
8．设
.表示三种不同的物体，用天平比较它们质量的大小，情况如图，那么这三种物体按质量从大到小的顺序为（ ） 
9．庐城出租车的收费标准：起步价４元(即行使距离不超过3千米都须付４元车费),超过3千米以后,每增加1千米,加收2元(不足1千米按1千米计)．某人乘出租车从甲地到乙地共付车费18元,那么甲地到乙地路程是( )
A． 9.5千米 B． 10千米 C． 至多10千米 D．至少９千米
10．某种商品的进价为800元，出售时标价为1200元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于5%，则至少可打（ ）
A．6折 B．7折 C．8折 D．9折
二、填空题（每小题４分，共40分）
11．已知x的与5的差不小于3，用不等式表示这一关系式为
．
12．某饮料瓶上有这样的字样：Eatable Date 18 months. 如果用x （单位：月）表示Eatable Date（保质期），那么该饮料的保质期可以用不等式表示为 ．
13．当x
时，式子3x5的值大于5x + 3的值。
14．阳阳从家到学校的路程为2400米，他早晨8点离开家，要在8点30分到8点40分之间到学校，如果用x表示他的速度（单位：米/分），则x的取值范围为 ．
15．若不等式
<
的解集为x>－2,则
=_______．
16．若不等式组
有解,则m的取值范围是________．
17．若ａ＞ｂ，不等式组
的解集为 ．
18．一次普法知识竞赛共有30道题，规定答对一道题得4分，答错或不答，一道题得－1分，在这次竞赛中，小明获得优秀（90或90分以上），则小明至少答对了 道题．
19．当ａ为 时，不等式组
的解集只有一个元素．
20．ａｇ糖水中有ｂｇ糖（ａ>ｂ>０），则糖的质量与糖水的质量比为 ；若再添加ｃｇ糖（ｃ＞０），则糖的质量与糖水质量的比为 ；生活常识告诉我们：添加的糖完全溶解后，糖水会更甜，请根据所列式子及这个生活常识提炼出一个不等式：
．
三、解下列不等式（组）（共12分）
21．(5分)解不等式
，并把它的解集表示在数轴上。
22．（７分）解不等式组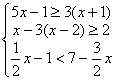
四、想一想（每小题9分，共18分）
23．已知方程组
，为何值时，
＞
？
24．有一个两位数，其十位数字比个位数字大2，这个两位数在50和70之间，你能求出这个两位数吗？
五、实际应用（每小题10分，共40分）
25．小颖家每月水费都不少于15元，自来水公司的收费标准如下：若每户每月用水不超过5立方米，则每立方米收费1. 8元；若每户每月用水超过5立方米，则超出部分每立方米收费2元，小颖家每月用水量至少是多少？
26．学校将若干间宿舍分配给七年级一班的女生住宿，已知该班女生少于35人，若每个房间住5人，则剩下5人没处住；若每个房间住8人，则空一间房，并且还有一间房也不满。有多少间宿舍，多少名女生？
27．足球比赛的记分规则为：胜一场得3分，平一场得1分，输一场得0分。一支足球队在某个赛季中共需比赛14场，现已比赛了8场,输了1场，得17分。
请问：
(1)前8场比赛中,这支球队共胜了多少场？
(2)这支球队打满14场比赛,最高能得多少分?
(3)通过对比赛情况的分析,这支球队打满14场比赛,得分不低于29分,就可以达到预期的目标.请你分析一下,在后面的6场比赛中,这支球队至少要胜几场,才能达到预期目标?
28．阅读下列材料：十六大提出全面建设小康社会，国际上常用恩格尔系数n来衡量一个国家和地区人民生活水平的状况，它的计算公式为：
n＝
各类家庭的恩格尔系数如下表所示：
| 家庭类型 | 贫困 | 温饱 | 小康 | 富裕 | 最富 |
| n | n>60% | 50%<n≤60% | 40%<n≤50% | 30%<n≤40% | n≤30% |
根据上述材料，解答下列问题：
某校初三学生对某乡的农民家庭进行抽样调查，从1997年至2002年间，该乡每户家庭消费支出总额每年平均增加500元，其中食品消费支出总额每年平均增加200元，1997年该乡农民家庭平均刚达到温饱水平，已知该年每户家庭消费支出总额平均为8000元。
(1)1997年该乡平均每户家庭食品消费支出总额为多少元？
(2)设从1997年起m年后该乡平均每户的恩格尔系数为nm(m为正整数)，请用m的代数式表示该乡平均每户当年的恩格尔系数nm，并利用这个公式计算2003年该乡平均每户的恩格尔系数（百分号前保留整数）。
(3)按这样的发展，该乡将于哪年开始进入小康家庭生活？该乡农民能否实现十六大提出的2020年我国全面进入小康社会的目标？