八年级数学上学期期中试卷
班级 姓名 学号
一.填空题（每小题2分，共18分）
1. 如果点P(2.k)在直线
上，那么k的值是 .
2．直线
可由直线
向
平移 个单位得到，它经过 象限.
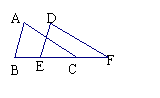3．如图，已知∠ABC=∠DEF，AB=DE，要说明△ABC≌△DEF若以“SAS”为依据，还要添加的
条件为______________．
第3题图
4．已知一次函数
，函数
的值随
值的增大而增大，则
的取值范围
是 ．
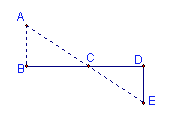
5．如图所示：要测量河岸相对的两点A、B之间的距离，先从B处出发与AB成90°角方向，向
前走50米到C处立一根标杆，然后方向不变继续朝前走50米到D处，在D处转90°沿DE
方向再走17米，到达E处，使A、C与E在同一直线上，那么测得A、B的距离为_____米．
6．如图所示是温度计的示意图，左边的刻度表示摄氏温度，℉右边的刻
度表示华氏温度华氏（℉）温度y与摄氏（℃）温度x之间的函数关系
式为___ _.
7．把一组64个数据的样本分成8组，从第一组到第四组的频数分别为5、
7、11、13，第五组到第七组的频率都是0.125，则第八组的频率
为 ．
第6题图
8．如图是某校八年级一班50名学生的一次数学测验成绩的扇形统计图，按图中划分的分数段，
这次测验成绩中70——79分所占百分比是_______．
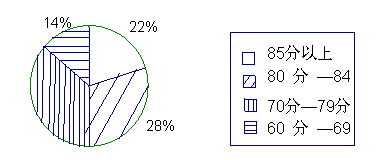
第8题图
9．已知直线
与轴,轴围成一个三角形,若这个三角形面积为3平方单位，则m的
值是 .
二、选择题（每小题2分，共18分）
10．函数
中，自变量x的取值范围是（ ）
A．x≥－1 B．x＞0 C．x≥－1且x≠0 D．x＞－1且x≠0
11．已知函数y=3x+1，当自变量增加m时，相应的函数值增加( ).
A．3m+1 B．3 m C． m D．3 m -1
12．一次函数y=（1-k）x+k，若k＞1，则函数图象不经过（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
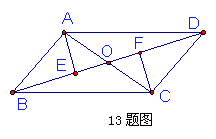
13．如图所示，已知AB∥CD，AD∥BC，AC与BD交于点O，AE⊥BD于E，CF⊥BD于E，
图中全等三角形有（ ）
A．3对 B．5对 C．6 对 D．7对
14．某校把七年级320名女生的体重情况进行调查后绘制成扇形统计图，发现体重在40㎏—50㎏对应的扇形圆心角为126°，则体重在40㎏—50㎏范围内的女生有（ ）
A．126人 B．112人 C．124人 D．198人
15．下列图形中，表示一次函数y = mx + n与正比例函数y = mnx（m、n为常数，且mn≠0）的图象的是 （ ）
 |
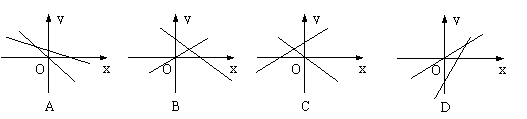16．中央电视台在今年六月份某一天发布的天气预报显示我国内地31个直辖市和省会城市的最高气温（0C）情况如下表：
| 气温（0C） | 18 | 21 | 22 | 23 | 24 | 25 | 27 | 28 | 29 | 30 | 32 | 33 | 35 | 36 |
| 城市数 | 1 | 1 | 1 | 3 | 1 | 3 | 1 | 5 | 4 | 3 | 1 | 4 | 1 | 2 |
那么能够显示这些城市在这一天数据的分布情况，可绘制（ ）
A．条形图 B．扇形图 C．折线图 D．直方图
18题图
17．右图中两条直线
和
和交点坐标可以看作下列方程组中（ ）的解。
A . 
B.
C.
D.
18.如图，在
中，
，
于D，
㎝，AD=6㎝,则
的长是（ ）
A.2㎝ B.1.5㎝ C.1㎝ D.3㎝
三. 解答题
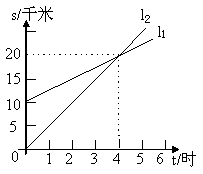19、（9分）如图，
反映了甲离开A的时间与离A地的距离的关系，
反映了乙离开A地的时间与离A地的距离之间的关系，根据图象填空：
（1）当时间为2小时时，甲离A地 千米，
乙离A地 千米。
（2）当时间为6小时时，甲离A地 千米，
乙离A地 千米．
（3）当时间 时，甲、乙两人离A地距离相等。
（4）当时间 时，甲在乙的前面，
当时间 时，乙超过了甲．
（5）对应的函数表达式为
，对应的函数表达式为
．
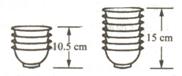
20、（6分）两摞相同规格的饭碗整齐地叠放在桌面上，请根据图中给出的数据信息，解答问题：
（1）求整齐叠放在桌面上饭碗的高度y（cm）与饭碗数x（个）之间的一次函数解析式（不要求写出自变量x的取值范围）；
（2）若桌面上有12个碗，整齐叠放成一摞，求出它的高度。
21、（7分）为了了解某初中学生的体能情况，抽取若干名学生在单位时间内进行引体向上测试，将所得数据整理后，画出频数分布直方图（如图），图中从左到右依次为第1、2、3、4、5组．
（1） 求抽取多少名学生参加测试？
（2） 处于哪个次数段的学生数最多？（答出是第几组即可）
（3） 若次数在5次（含5次）以上为达标，求这次测试的达标率．
 |
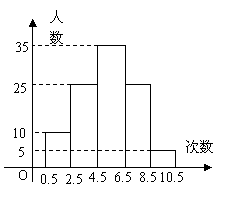22．（8分）如图，在△ＡＢＣ中，点Ｄ在ＡＢ上，点Ｅ在ＢＣ上，ＢＤ＝ＢＥ。
（１）请你再添加一个条件，使得△ＢＥＡ≌△ＢＤＣ，并给出证明。
你添加的条件是：___________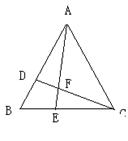 
（２）根据你添加的条件，再写出图中的一对全等三角形：____________（只要求写出一对全等三角形，不再添加其他线段，不再标注或使用其他字母，不必写出证明过程）
四．多项选择题（6分）
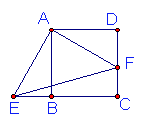
23．如图，将△ADE绕正方形ABCD的顶点A顺时针旋转90度，
得到△ABF，连结EF，则下列结论正确的是（ ）
A．△ADE≌△ABF B．AE⊥AF
C．∠AEF=45° D．四边形AECF的周长等于ABCD的周长
24. 如图3是一名同学骑自行车出行的图象，从图象得知
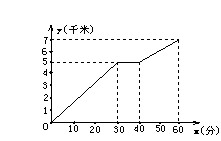正确的信息是（ ）
A．整个行进过程中的路程是7千米
B．前30分钟的速度比后20分钟速度快4千米/时
C．该同学在途中停下来休息了10分钟
D．该同学从起点到终点的平均速度是7千米/时
五．证明或解答
25. （8分）已知，如图，A，E，F，C在同一条直线上，AE=CF，过E，F分别作DE⊥AC，BF⊥AC，垂足分别是E，F，连接BD交AC于G，若AB=CD.
（1） 试证：BG=DG ;
（2） 若将⊿ABF的边AF沿CA方向平移为图乙时，其余条件不变，BG=DG是否成立？
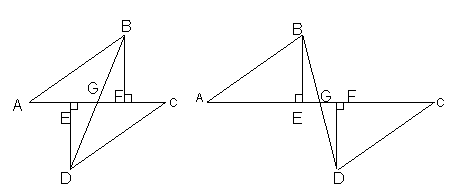
（甲） （乙）
26、（9分）北京某厂和上海某厂同时制成某大型机器若干台，北京厂可支援外地10台，上海厂可支援外地4台，现在决定给重庆8台，汉口6台。如果从北京运往汉口、重庆的运费分别是400元/台、800元/台，从上海运往汉口、重庆的运费分别是300元/台、500元/台。
求：(1)设上海运往汉口台，总运费为元，求与的函数关系式；
(2)若要求总运费不超过8200元，共有几种调运方案?
(3)求出总运费最低的调运方案，最低总运费是多少元?
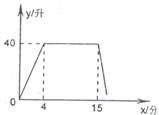
27、（9分）某洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续过程，其中进水、清洗、排水时洗衣机中的水量y（升）与时间x（分钟）的关系如折线图所示：
根据图象解答下列问题：
（1）洗衣机的进水时间是多少分钟？清洗时洗衣机中的水量是多少升？
（2）已知洗衣机的排水速度为每分钟19升，
①求排水时y与x之间的关系。②如果排水时间为2分钟，求排水结束时洗衣机中剩下的水量。
