八年级数学单元同步调查测试二
平行四边形
班级 学号 姓名
一、填空(每题3分，共33分)
1、平行四边形ABCD中，若∠A的补角与∠B互余，则∠D的度数是 。
2、平行四边形ABCD的周长是18，三角形ABC的周长是14，则对角线AC的长是 。
3、矩形ABCD中，点E为边AB上的一点，过点E作直线EF垂直对边CD于F，若SAEFD：SBCFE=2：1，则DF：FC= 。
4、矩形的两条对角线的一个交角为60 o，两条对角线的和为8cm，则这个矩形的一条较短边为 cm。
5、菱形的一个内角为
,且平分这个内角的对角线长为8cm，则这个菱形的周长为
。
6、若正方形的一条角平分线m，则这个正方形的面积为 。
7、矩形的一条角平分线分长边为5cm和4cm两部分，则此面积为 。
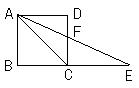8、正方形ABCD的边BC的延长线上
取一点E，使CE=AC，AE与CD交于
点F，则∠AFC= 。
9、梯形的上底长为2，下底长为5，一腰为4，则另一腰m的范围是 。
10、梯形ABCD中，AD∥BC，对角线AC=8cm,BD=6cm，且AC⊥BD，则梯形的面积为 。
11、等腰梯形两底的差等于底边上高的2倍，则这个梯形较小的底角为 度。
二、选择（每题3分，共24分）
1、平行四边形的一边长为10cm，那么这个平行四边形的两条对角线长可以
是 （ ）
A、4cm和 6cm B、6cm和 8cm
C、 20cm和 30cm D8cm 和12cm
2、给定不在同一直线上的三点，则以这三点为顶点的平行四边形有（ ）
A、1个 B、2个 C、3个 D、4个
3、如图，AE∥BD， BE∥DF， AB∥CD，下面给出四个结论
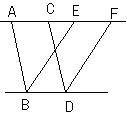（1）AB=CD （2）BE=DF
（3）SABDC=SBDFE
（4）S△ABE=S△DCF 其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个
4、平行四边形ABCD的对角线AC、BD相交于点O，
下列条件中，不能判定它为菱形的是 （ ）
A、AB=AD B、AC⊥BD C、∠A=∠D D、CA平分∠BCD
5、正方形具有而菱形不一定具有的性质是 （ ）
A、四条边都相等 B、对角线相等
C、对角线互相垂直平分 D、每条对角线平分一组对角
6、下列四边形中，既是中心对称图形，又是轴对称图形，而且有四条对称轴的是 （ ）
A、平行四边形 B、矩形 C、菱形 D、正方形
7、能识别四边形ABCD是等腰梯形的条件是 （ ）
A、AD∥BC，AB=CD B、∠A：∠B：∠C：∠D=3：2：3：2
C、AD∥BC，AD≠BC，AB=CD D、∠A+∠B=180o，AD=BC
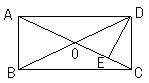8、如图，矩形ABCD中，DE⊥AC于E，且
∠ADE：∠EDC=3：2，则∠BDE的度数为（ ）
A、36o B、18o C、27o D、9o
三、解答题
1、平行四边形的周长为20cm ，AE⊥BC于E，AF⊥CD于F，AE=2 cm，AF=3 cm，求平行四边形ABCD的面积。（5分）
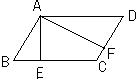
2、如图，菱形ABCD中，BE⊥AD，BF⊥CD，E、F为垂足，AE=ED，求
∠EBF的度数。（6分）
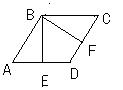
3、如图，已知在直角梯形ABCD中，BC∥AD，AB⊥AD，底AD=6，斜腰CD的垂直平分线EF交AD于G，交BA的延长线于F，且∠D=45o，求BF的长度。(6分)
4、已知：正方形ABCD，以AD为边作等边三角形ADE，求∠BEC的度数。（要求画出图形，再求解）（8分）
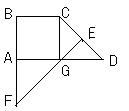
5、如图，等腰三角形ABC中，D是BC边上的一点，DE∥AC，DF∥AB，通过观察分析线段DE，DF，AB三者之间有什么关系？试说明你的对结论。（6分）
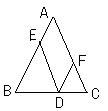
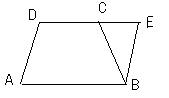
6、在梯形ABCD中，DC∥AB，E是DC延长线上一点，BE∥AD，BE=BC，∠E=50o，试求梯形ABCD的各角的度数。请问此时梯形ABCD是等腰梯形吗？为什么？（6分）
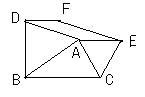
7、如图，以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE，四边形ADFE是平行四边形（6分）
（1） 当∠BAC满足什么条件时，四边形ADFE是矩形？
（2） 当∠BAC满足什么条件时，平行四边形ADFE不存在？
（3） 当△ABC分别满足什么条件时，平行四边形ADFE是菱形，正方形？
