上学期第一次月考试卷
初 二 数 学
满分:100 时间:100分钟
班级______________姓名__________________成绩____________________
一．选择题（每题3分，共30分）
1、下列函数（1）y=
x (2)y=2x-1 (3)y=
(4)y=2-3x (5)y=x2-1中，是一次函数的有（ ）
A、4个 B、3个 C、2个 D、1个
2、在一次函数y=kx+3中，当x=3时，y=6，则k的值为（ ）
A、-1 B、1 C、5 D、-5
3、过点（2，3）的正比例函数解析式是（ ）
A、y=
B、y=
C、y=2x-1 D、y=
4．已知点（-4，y1），（2，y2）都在直线y=- x+2上，则y1 与y2大小关系是( )
A、y1 >y2 B、y1 =y2 C、y1 <y2 D、不能比较
5、已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
 |  |  |  | ||||
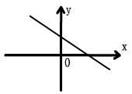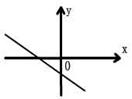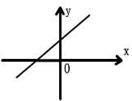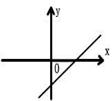(A) (B) （C） （D）
6、下列说法正确的是（ ）
A、一次函数是正比例函数 B、正比例函数包括一次函数
C、一次函数不包括正比例函数 D、正比例函数是一次函数
7、直线y=2x–1与 y=–x+3 交点一定在 （ ）
A第一象限 B第二象限 C第三象限 D第四象限
8、下面函数图象不经过第二象限的为 （ ）
A、 y=3x+2 B、 y=3x－2 C、 y=－3x+2 D、 y=－3x－2
8、一次函数y = kx + b，当– 3≤x≤1时，对应的y值为1≤y≤9，则kb的值为（ ）
A、14 B、– 6 C、– 1或21 D、– 6或14
9、一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度n(厘米)与燃烧时间t(时)的函数关系的图象是( )
 |
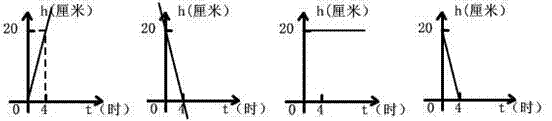(A) (B) （C） （D）
二、填空（每题3分，共30分）
11、若函数y=x+a-1是正比例函数，则a= 。
12、若关于x的函数y﹦﹙n﹢1﹚xm﹣1是一次函数，则m= ，n 。
13、把y=2x+1向左移动两个单位可得到直线解析式 。
14、一次函数y= -2x+4的图象与x轴交点坐标是 ，与y轴交点坐标是 , 图象与坐标轴所围成的三角形面积是 .
15、某商店出售一种瓜子，其售价y（元）与瓜子质量x（千克）之间的关系如下表
| 质量x（千克） | 1 | 2 | 3 | 4 | …… |
| 售价y（元） | 3.60+0.20 | 7.20+0.20 | 10.80+0.20 | 14.40+0.2 | …… |
由上表得y与x之间的关系式是 .
16、已知一个正比例函数的图象经过点（-2，4），问点（
，
）是否在图象上？答
17、我国是一个严重缺水的国家，大家都应倍加珍惜水资源，节约用水。据测试，拧不紧的水龙头每秒钟滴下2滴水，每滴水约0.05毫升，小明同学洗手时，没有把水龙头拧紧，当小明离开x小时后，水龙头滴y毫升的水，试写出y关于x的函数关系式 .
18、已知函数
的图像经过点（1，－2），且y随自变量x的增大而减小，写出一个满足上述条件的函数解析式
19、如果直线y=mx+n经过一、二、三象限，
那么mn 0。(填“>” “<”或“=”)
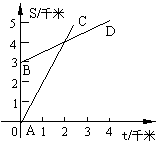20、如图，已知A地在B地正南方3千米处，甲乙两人同时分别从A、B两地向正北方向匀速直行，他们与A地的距离S（千米）与所行的时间t（小时）之间的函数关系图象如图所示的AC和BD给出，当他们行走3小时后，他们之间的距离为
千米.
三、解答题（共40分）
21、（8分）已知函数y= mx﹢n经过A（4，-7），B（-4，5）两点，
求这个函数的解析式。
22、（12分）画出函数y=2x+6的图象，利用图象：
（1）求方程2x+6=0的解； （3分）
（2）求不等式2x+6＞0的解； （3分）
（3）若-1≤y≤3，求x的取值范围。 （3分）
（3）利用图象解方程组：
24、（10分）如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题：
(1)当行驶8千米时,收费应为 元;
(2)从图象上你能获得哪些信息?(请写出2条)
①
②
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.
4、（10分）某饮料厂为了开发新产品，用A、B两种果汁原料各19千克、17.2千克，试制甲、乙两种新型饮料共50千克，下表是试验的相关数据：
| 饮料 每千克含量 | 甲 | 乙 |
| A（单位：千克） | 0.5 | 0.2 |
| B（单位：千克） | 0.3 | 0.4 |
（1） 假设甲种饮料需配制x千克，请你写出满足题意的不等式组，并求出其解集.
（4分）
（2）设甲种饮料每千克成本为4元，乙种饮料每千克成本为3元，这两种饮料的成本总额为y元，请写出y与x的函数表达式.并根据（1）的运算结果，确定当甲种饮料配制多少千克时，甲、乙两种饮料的成本总额最少，最少成本是多少？（6分）