初二数学第一学月学情检测
(时间90分钟 满分100)
一.选择.(3′×12=36′)
1.已知函数![]() 是一个一次函数,则
是一个一次函数,则![]() 的值为( )
的值为( )
A.1 B.-1 C.1或-1 D.0或-1
2.下列函数中,自变量![]() 的取值范围是
的取值范围是![]() >2的函数是( )
>2的函数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.一次函数![]() 的图象不经过( )
的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
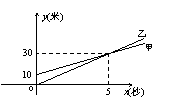 4.甲、乙进行跑步训练的情况如图,6秒时,下列说法正确的是( )
4.甲、乙进行跑步训练的情况如图,6秒时,下列说法正确的是( )
A.甲在乙前
B.乙在甲前
C.甲、乙相遇
D.不能确定
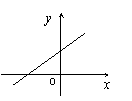 5.(2007·福州)已知一次函数
5.(2007·福州)已知一次函数![]() 的图象如图所示,则
的图象如图所示,则![]() 的取值范围是( )
的取值范围是( )
A.![]() >1
>1
B.![]() <1
<1
C.![]() >0
>0
D.![]() <0
<0
6.(书P281#)下列函数中是一次函数的有( )个
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
A.1 B.2 C.3 D.4
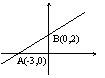 7.(2007·海南有改动)如图一次函数
7.(2007·海南有改动)如图一次函数![]() 的图象过A、B两点,则
的图象过A、B两点,则![]() 的解集是( )
的解集是( )
A.![]() <0
B.
<0
B.![]() <2
<2
C.![]() <-3
D.-3<
<-3
D.-3<![]() <2
<2
|
8.已知直线![]() 上有两点(2,
上有两点(2,![]() ),(5,
),(5,![]() ),则
),则![]() 与
与![]() 的关系是( )
的关系是( )
A.![]() >
>![]() B.
B.![]() <
<![]() C.
C.![]() =
=![]() D.无法确定
D.无法确定
9.(创P133#)一次函数![]() 过点(3,-5),那么它的图象还经过( )
过点(3,-5),那么它的图象还经过( )
A.(0,-1) B.(-2,3) C.(1,0) D.(2,-3)
10.(书P196# 变式)下列各曲线中![]() 不是
不是![]() 的函数的是( )
的函数的是( )
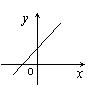 | 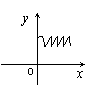 | 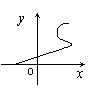 | 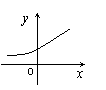 |
A. B. C. D.
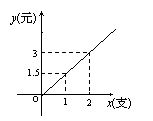
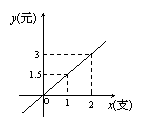
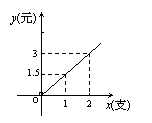
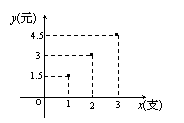 11.小明去买铅笔,每支单价为1.5元,他所用钱
11.小明去买铅笔,每支单价为1.5元,他所用钱![]() (元)与支数
(元)与支数![]() (支)之间的函数关系如下图是( )
(支)之间的函数关系如下图是( )
 A.
B.
C.
D.
A.
B.
C.
D.
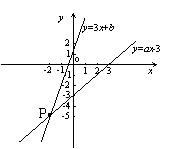
12.(2007·武汉有改动)如图,已知函数![]()
和![]() 的图象交于点P(-2,-5),则根据图象可
的图象交于点P(-2,-5),则根据图象可
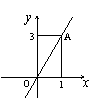 得不等式
得不等式![]() 的解集是( )
的解集是( )
A.![]() <-2
B.
<-2
B.![]() >-2
C.
>-2
C.![]() <-5
D.
<-5
D.![]() >-5
>-5
二.填空.(3′×6=18′)
13.(2007·上海)如图,正比例函数图象经过点A,该函数解析式
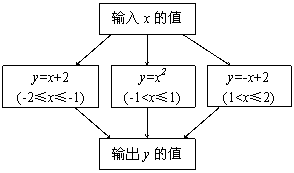 是
.
是
.
14.(创P210#)如图是计算某函数值
的程序示意图,若输入![]() 的值为
的值为![]() ,
,
则输出的结果为 .
15.某一次函数的图象经过点(-1,3),
且![]() 随
随![]() 的减小而减小,请写一个符合
的减小而减小,请写一个符合
上述条件的函数关系式为 .
16.当![]() 时,直线
时,直线![]() 上的点在
上的点在![]() 轴下方.
轴下方.
17.将直线![]() 向下平移5个单位长度后的直线解析式为
.
向下平移5个单位长度后的直线解析式为
.
18.我市出租车收费标准是:1km以内4元钱,每超过1km每公里多收1.2元,若![]() 表示所付费用(元),
表示所付费用(元),![]() 表示所走公里数,则
表示所走公里数,则![]() 关于
关于![]() 的函数关系式是
的函数关系式是
.
三.解答.(共46′,其中22题6′,其余各题8′)
19.(书P282#变式)一个小球在一个斜坡上向下滚动,若它的初始速度是1米/秒,以后速度每秒增加2米/秒.
⑴求小球速度![]() 随时间
随时间![]() 变化的函数关系式;
变化的函数关系式;
⑵求第3秒时小球的速度.
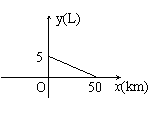
20.(书P9例1)一辆汽车的油箱中现有油5L,如果不再加油,那么油箱中的油量![]() (单位:L)随行驶里程
(单位:L)随行驶里程![]() (单位:km)的增加而减少,平均耗油量为0.1L/km.
(单位:km)的增加而减少,平均耗油量为0.1L/km.
⑴写出表示![]() 与
与![]() 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
⑵江油—绵阳为38km,请问从江油走到绵阳能否不加油?
⑶请作出该函数的图象.
|
21.(书P33例6变式)由于国家扶持养猪事业,广元、旺苍两地现急需肥料,我市某厂有肥料300吨,需全部调往两地,已知从我市运往广元、旺苍的费用分别为每吨15元与20元,若广元最多需要100吨,怎样调运费最少?请用函数的观点解释.
22.(书P38引入)用函数图象解方程![]() .
.
23.若某直线经过点A(3,0),且它与两坐标轴围成的三角形面积为6,求该直线的解析式.
24.(创P88#,书P356# 变式)已知![]() 与
与![]() 成正比例,若
成正比例,若![]() 随
随![]() 的增大而减少,且其图象经过A(1,
的增大而减少,且其图象经过A(1,![]() ),和B(
),和B(![]() ,-1)两点,求
,-1)两点,求![]() 和
和![]() 之间的函数解析式.
之间的函数解析式.
答案:
一.选择.
1.B 2.C 3.C 4.B 5.A 6.B 7.C 8.A 9.D 10.C 11.C 12.B
二.填空.
13.![]() 14.
14.![]() 15.答案不唯一,如
15.答案不唯一,如![]() 16.>-3
16.>-3
 17.
17.![]() 18.
18.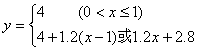 或
或![]()
19.⑴v=1+2t ⑵当t=3时,v=7m/秒
20.⑴![]() ⑶
⑶
⑵ ∵ 38<50 ∴ 可以不加油
21.设调往广元![]() 吨,
吨,![]() (0<x≤100=
(0<x≤100=
∵![]() ∴
∴ ![]() 随
随![]() 增大而减小 ∴ 当
增大而减小 ∴ 当![]() =100时
=100时
 y嗫小=6000-5×100=5500(元)
y嗫小=6000-5×100=5500(元)
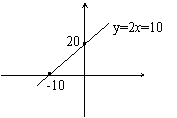
22.⑴令![]() ⑵作出函数图象
⑵作出函数图象
⑶依图知直线与![]() 轴交点是(-10,0)
轴交点是(-10,0)
∴ 原方程的解为![]() =-10
=-10
23.![]() 或
或![]()
24.![]()