八年级数学（上）期中考试

八年级数学（上）期中考试

八年级数学试卷

一、选择题（本大题共5小题，每小题3分，共15分）在每小题给出的四个选项中，只有一个是正确的，请将所选选项的字母写在题目后面的括号内。

1．用圆的半径r来表示圆的周长C，其式子为C＝2πr。则其中的常量为（　 ）

　 A．r　　　　　  B．π　　　　　  C．2　　　　　  D．2π

2．已知下列各式： ① y＝3x＋5　　② y＝－3x＋5　　③ y＝3x²＋5　

 ④ y＝－2x在这些式子中，y是x的一次函数的是 　　　　　　　　　（　 ）

　 A．①②　　　　 B．②④　　　　  C．①②③　　　 D．①②④

3．反映某种股票的涨跌情况应选择　　　　　　　　　　　　　　　　 （　 ）

　 A．扇形图　　　 B．折线图　　　　C．直方图　　　 D．都可以

4．已知△ABC≌△A′B′C′，且△ABC的周长为20，AB＝8，BC＝5，那么

A′C′等于　　　　　　　　　　　　　　　　　 　　　　　　　 （　 ）

　 A．5　　　　　  B．6　　　　　　 C．7　　　　　  D．8

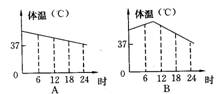
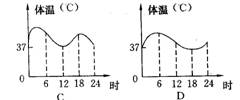
5．一天,亮亮发烧了,早晨他烧得厉害,吃过药后感觉好多了, 中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜亮亮才感觉身上不那么烫了。图中能基本上反映出亮亮这一天(0时～24时)体温的变化情况的是　　　 (　 )

二、填空题（本大题共5小题，每小题4分，共20分）请把下列各题的正确答案填写在横线上。

6．函数y＝5x－9是　　   函数， y随x的增大而　　　　 。

7．当x＝－1时，函数y＝kx＋3的值为5，则k＝　　　　。

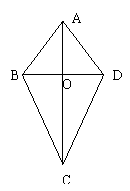8．如图，在△ABC和△FED中，AD＝FC，AB＝EF，当添加条件　　　　　时，就可得到△ABC≌△FED（只需填写一个你认为正确的条件）

 

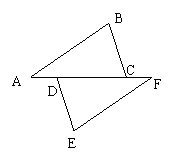
9．如图，AC⊥BD于O，OB＝OD，图中共有全等三角形　　　　对。

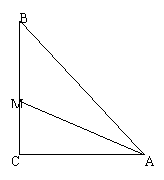
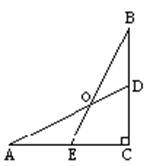
10．如图，在△ABC中，∠C＝90°，AM平分∠CAB，CM＝20cm，那么点M到AB的距离是　　　　cm。

三、解答题（本大题共5小题，每小题6分，共30分）

11．已知正比例函数y＝kx，当x＝－2时，y＝1，求当x＝时的y值。

12．某班学生参加的各项课外活动小组的人数情况如图所示，问：

　  ⑴ 哪种活动最受学生欢迎？

　  ⑵ 若该班共有50名学生，则参加文娱活动的有多少人？

　  ⑶ 图中表示参加文娱活动人数的扇形的圆心角是多少度？

13．在Rt△ACD和Rt△BCE中,若AD=BE,DC=EC,

⑴从中得到什么结论：　　　　　　　　　　  　　　（至少写两个结论）

⑵你证明其中的一个结论！

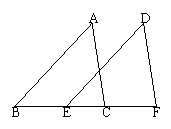
14．如图，点B，E，C，F在一条直线上，AB=DE，AC=DF，BE=CF，求证:∠A=∠D.

15．学校阅览室有能坐4人的方桌，如果多于4人，就把方桌拼成一行，2张方桌拼成一行能坐6人，如图所示，请你结合这个规律，填写下表并回答问题：

拼成一行的方桌数	1	2	3	4	……
人数	4	6	8		……

.

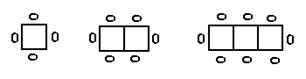
若初二（1）班有42人去阅览室看书，那么需要多少张方桌（即求值）？

四、解答题（本大题4小题，每小题7分，共28分）

16．一个弹簧不挂重物时长12 cm，挂上重物后伸长的长度与所挂重物的质量成正比；如果挂上1 kg的物体后，弹簧伸长2 cm；求弹簧总长度y（单位：cm）随所挂物体质量x（单位：kg）变化的函数关系式。

17．已知一组数据：25、21、23、25、27、29、25、28、30、29、26、24、25、27、26、22、24、25、26、28

　 ⑴ 填写下面的频数统计表：

分组（含最小值，不含最大值）	21—23	23—25	25—27	27—29	29—31
划记
频数

　 ⑵ 绘制频数直方图

18．已知一次函数的图象过点A（－3，2），B（1，6）

　  求：⑴函数解析式；　　⑵函数图象与坐标轴围成的三角形面积。

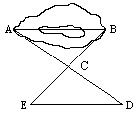
19．如图,有一池塘,要测池塘两端A、B的距离，可先在平地上取一个可以直接到达A和B的点C，连结AC并延长到D，使CD=CA；连结BC并延长到E，使EC=CB；连结DE，量出DE的长就是A、B的距离，为什么？

五、解答题（本大题共3小题，每小题9分，共27分）

20．某中学团委会为研究该校学生的课余活动情况，采取抽样的方法，从阅读、运动、娱乐、其它等四个方面调查了若干名学生的兴趣爱好，并将调查的结果绘制了如下的两幅不完整的统计图（如图1,图2），请你根据图中提供的信息解答下列问题：

（1）在这次研究中，一共调查了多少名学生？

（2）“其它”在扇形图中所占的圆心角是多少度？

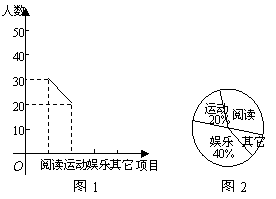（3）补全频数分布折线图．

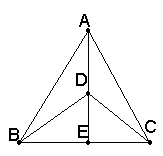
21．已知△ABC中， AE为角平分线，D为AE上一点，且∠BDE=∠CDE，

（1）求证：AB=AC

（2）若把 “AE角平分线”换为“AE为高线”，其它条件不变，结论还会成立吗？如果成立，请证明；若不成，请说明理由.

22．已知：在直角坐标系中，直线 与轴交于点，与轴交于点。

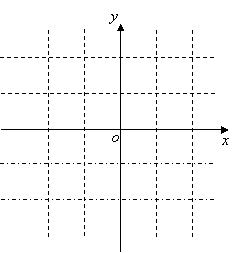
⑴画出这个函数的图象，并直接写出两点的坐标；

⑵若点是第二象限内的点，且到轴的距离为1，到轴的距离为，请判断点是否在这条直线上？（写出判断过程）

⑶在第⑵题中，作轴于，那么在轴上是否存在一点，使△≌△？若存在，请直接出点的坐标；若不存在，请说明理由。

六、附加题（20分）

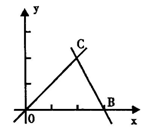
如图，直线OC、BC的函数关系式分别是y₁=x和y₂=-2x+6，动点P（x，0）在OB上运动（0<x<3），过点P作直线m与x轴垂直．

　（1）求点C的坐标，并回答当x取何值时y₁>y₂？

　（2）设△COB位于直线m左侧部分的面积为s，求出s与x之间函数关系式．

　（3）当x为何值时，直线m平分△COB的面积？