八年级数学（上）全等三角形单元检测题
（时间：90分钟；满分100分）
班别____________姓名_________________分数__________
一、填空题（每小题3分,共24分）.
1. 如图（1）,AC、BD相交于点O，△AOB≌△COD，∠A＝∠C，则其他对应角分别是＿＿＿＿＿＿＿＿＿＿＿＿＿；对应边分别为＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿．
2. 如图（2），在△ABＣ中，∠C＝90°，AD平分∠BAC,BC=10㎝,BD=6㎝,则点D到AB的距离为＿＿＿＿㎝．
3.
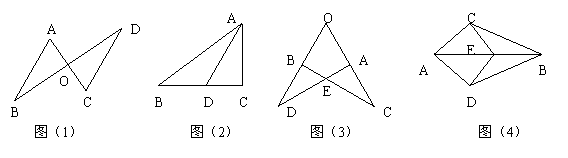如图（３），若△ＯAD≌△OBC，且∠O=65°，∠C=20°,则∠OAD=＿＿＿＿＿＿．
4. 如图（４），点Ｅ在ＡＢ上，ＡＣ＝ＡＤ，请你添加一个条件，使图中存在全等三角形，并给予证明．所添条件为＿＿＿＿＿＿＿＿＿＿＿；你得到的一对全等三角形是＿＿＿＿＿＿＿＿＿＿＿．
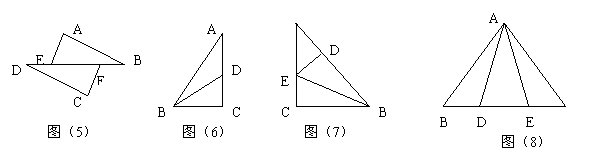
5. 如图（５），ＡＢ∥ＣＤ，ＡＥ∥ＣＦ，ＡＥ＝ＣＦ，ＢＤ＝12，ＢＦ＝2，则ＥＦ＝＿＿＿＿＿＿＿．
6. 如图（６），在Rt△ABC中, ∠C＝90°,ＢＤ是∠ＡBＣ的平分线，交ＡＣ于Ｄ，若ＣＤ＝４，ＡＢ＝８，则△ABD的面积是＿＿＿＿＿＿＿＿．
7. 如图（７），Rt△ABC中, ∠C＝90°,ＢＣ＝３，ＡＣ＝４，ＡＢ＝５，ＢＥ平分∠ＡＢＣ，ＥＤ⊥ＡＢ，则△AＤＥ的周长为＿＿＿＿＿＿．
8.
已知三角形两边长为５和７，则第三边上的中线长m的取值范围是＿＿＿＿＿＿
_.
二、选择题（每小题3分,共24分）．
9. 如图（８），△ABE≌△ACD，ＡＢ＝ＡＣ，ＢＥ＝ＣＤ，∠Ｂ＝50°，∠AEC=120°,则∠DAC=（ ）.
（A）120° （B）70° （C）60° （D）50°
10. 使两个直角三角形全等的条件是（ ）.
（A）一锐角对应相等; （B）两锐角对应相等;
（C）一条边对应相等; （D）两条边对应相等.
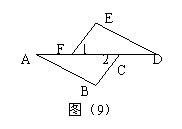
11. 
如图（9），已知∠A=∠D,, ∠1=∠2,那么要得到△ABC≌△DEF，还应给出的条件是（ ）.
（A）∠Ｅ＝∠B （B）ＥＤ＝ＢＣ
（C）ＡＢ＝ＥＦ （D）ＡＦ＝ＣＤ
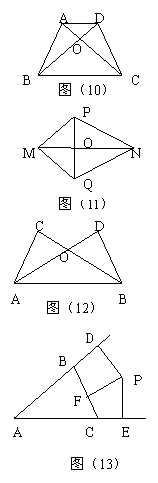
12. 如图（１０），ＡＤ∥ＢＣ，ＡＢ＝ＤＣ，ＡＣ、ＢＤ相交于点Ｏ，则图中全等三角形共有（ ）
（A）1对 （B）2对 （C）3对 （D）4对
13. 如图（11），ＭＰ＝ＭＱ，ＰＮ＝ＱＮ，ＭＮ交ＰＱ于点Ｏ，则下列结论中不正确的是（ ）．
（Ａ）△ＭＰＮ≌△ＭＱＮ （Ｂ）ＯＰ＝ＯＱ
（Ｃ）ＭＯ＝ＮＯ （Ｄ）∠ＭＰＮ＝∠ＭＱＮ
14. 如图（12），∠CＡＢ＝∠ＤＢＡ，ＡＣ＝ＢＤ，则下列结论中不正确的是（ ）．
（Ａ）ＡＢ＝ＡＤ （Ｂ）ＣＯ＝ＤＯ
（Ｃ）∠C＝∠Ｄ （Ｄ）∠ＣＡＤ＝∠ＤＢＣ
15. 如图（13），Ｐ点到ＢＤ、ＢＣ、ＣＥ的距离相等，则下列关于Ｐ的判断正确的是（ ）．
①ＢＤ平分∠ＤＢC；②ＡＰ平分∠ＢＡC；③ＰＣ平分∠ＢCＥ．
（Ａ）① （Ｂ）①③
（Ｃ）②③ （Ｄ）①②③
16. 
如图（14），已知△ABC的六个元素，则下列甲、乙、丙三个三角形中和△BAC全等的图形是（ ）．
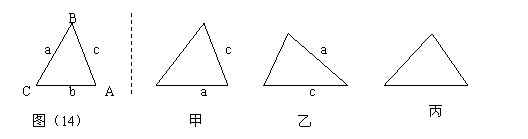（Ａ）甲和乙 （Ｂ）乙和丙 （Ｃ）只有乙 （Ｄ）只有丙
三、解答题（共４小题，每题13分,共52分）
17. 
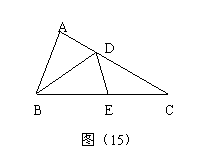如图（15），在△ABC中,ＡＤ＝ＤＥ，ＡＢ＝ＢＥ，∠Ａ＝８０°，求∠ＢＥＤ的度数．
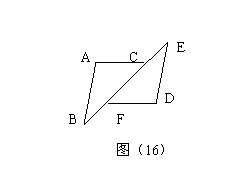
18. 如图（16），ＡＢ∥ＤＥ，ＢＦ＝ＥＣ，∠Ａ＝∠Ｄ．求证：ＡＣ＝ＤＦ．
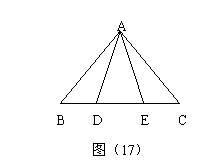
19. 如图（17），Ｄ、Ｅ在ＢＣ上，且ＢＤ＝ＣＥ，ＡＤ＝ＡＥ，∠ＡＤＥ＝∠ＡＥＤ．
求证：ＡＢ＝ＡＣ．
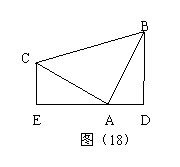
20. 如图（18），在△AＢＣ中，∠ＢＡC＝90°,ＡＢ＝ＡＣ，ＢＤ⊥ＤＥ，ＣＥ⊥ＤＥ，且ＤＥ过点Ａ．求证：ＤＥ＝ＢＤ＋ＣＥ．
