八年级数学第二学期期中试卷
时间：100分钟 试卷总分：120分 考试形式：闭卷
一、选择题：（每小题3分，共30分）
1、如果a>b ，下列各式中正确的是 ( )
A、a－3>b－3 B、
>
C、2-2a>2-2b
D、a－b <0
2、分式
与下列分式相等的是（ ）
A 、
B、 
C、
D、
3、函数
的图象经过点（－4，6），则下列各点中不在图象上的是（ ）
A、（3，8） B、（3，－8） C、（－8，－3） D、（－4，－6）
4、已知关于x的不等式2x+m>-5的解集如图所示，则m的值为 ( )
A．1 B．0
C．-1 D．-2
5、如果把分式
中的x和y都扩大2倍，即分式的值（ ）
A.扩大4倍； B.扩大2倍； C.不变； D.缩小2倍
6、若点P（2-a,a-3）在第四象限，则a的取值范围为 （ ）
A、a<2 B、a<3 C、2<a<3 D、以上都不对
7、亮亮准备用自己节省的零花钱买一台英语复读机. 他现在已存有55元，计划从现在起以后每个月节省20元，直到他至少有350元. 设x个月后他至少有350元，则可以用于计算所需要的月数x的不等式是
A.20x－55≥350 B.20x＋55≥350
C.20x－55≤350 D.20x＋55≤350
8、若关于x的方程
产生增根，则m是( )
A、-1 B、1 C、-2 D、2
9、函数
与函数
在同一坐标系中的大致图象是下图中的 （ ）
(A) (B) (C) (D)
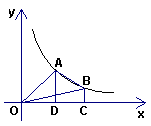10、如图，已知A、B两点是反比例函数y=
（x＞0）的
图象上任意两点. 过A、B两点分别作x轴的垂线，垂足分别
为D、C. 连接AB、AO、BO，则梯形ABCD的面积与△ABO的面
积比是
A.2∶1 B.1∶2
C.1∶1 D.2∶3
二、填空题：（每题3分，共24分）
11、不等式2x-1＜0的解集为 ；
12、当x 时，分式
的值为零；
13、
=
14、分式
、
、
的最简公分母是
；
15、若函数y=
是反比例函数，则m
。
16、不等式-3x＜7的负整数解为 ；
17、课堂上老师给出一个函数，甲、乙两名同学各指出了这个函数的一个性质：
甲同学：第二、四象限有它的图象；
乙同学：在每个象限内，y随x的增大而增大.
请你写出满足上述性质的一个函数_________________.
18、式子
叫做“行列式”，其展开方法是 ＝ad－bc（注意展开式中各项的符号）. 例如
＝2×3－(－1)×4＝10.若行列式
的值不小于－2，则y的取值范围是________________.
三、解答题：（本大题共46分）
19、解不等式及不等式组，（每小题5分，共10分）
（1）
（把解集在数轴上表示出来）
（2）
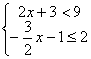
20、先化简，然后取一个你喜欢的数代入求值；（本题6分）
1－
÷ 
21、解方程； （本题6分）
22、（本题满分7分）已知函数y = y1 +y2，y1与x成正比例，y2与x成反比例，且当x = 1时，y =－1；当x = 3时，y = 5。求y关于x的函数关系式.
23、（本题8分）某项工程，若由甲队单独施工，刚好如期完成；若由乙队单独施工，则要超期3天。现甲乙两队同时施工2天后，剩下的工程由乙队独做，刚好如期完成。试问规定的工期是几天？
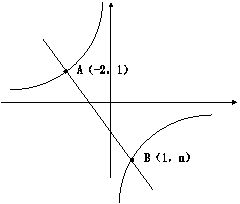
24、（本题9分）如图，一次函数
的图像与反比例函数
的图像相交于A、B两点，
（1）利用图中条件，求反比例函数和一次函数的解析式
（2）根据图像写出使一次函数的值大于反比例函数的值的
的取值范围
四、能力训练题（本大题20分）
25、（本题4分）如果关x的不等式(m-1)x>1-m的解集为x<-1，则m的取值范围是 。
26、（本题4分）已知点A（x
，y）,B（x
,y）和C（x
,y）都在反比例函数y
（k＜0）的图象上，且x＜0＜x＜x，则y、y、y的大小关系是 （ ）
A.y＞y＞y B.y＞y＞y C.y＞y＞y D.y＞y＞y
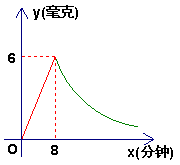
27、（本题12分）为了预防流感，某校对教室采用药熏消毒法进行消毒. 已知药物燃烧时，室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例；药物燃烧完后，y与x成反比例(如图). 现测得药物8分钟燃毕，此时室内空气中每立方米的含量为6毫克.请根据题目中所提供的信息解答下列问题：
（1）直接写出药物燃烧时及药物燃烧后y关于x的函数关系式.
（2）研究表明，当空气中每立方米的含药量低于1.6毫克时学生方可进教室，那么从消毒开始，至少需要经过多少分钟后学生才能回到教室？
（3）研究表明，当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？
 |