八年级数学上第十一章单元测试题
(满分100分，90分钟完卷)
姓名：____________ 得分：_________
一、选择题：（本大题共10个小题，每小题3分，共30分.）
1、下列函数 (1)
(2)
(3)
(4)
(5)
中，是一次函数的有（
）
A.4个 B.3个
C.2个 D.1个
2、函数
中自变量
的取值范围是 （ ）
A．
B.
C.
且 D.且
3、直线
,,
共同具有的特征是 （ ）
A.经过原点
B.与
轴交于负半轴
C.随增大而增大
D.随增大而减小
4、下列图中，不表示某一函数图象的是 （ ）
A B C D
5、下列各点在函数y=1－2x的图象上的是：（ ）。
（A）（2，－1） （B）（0，2） （C）（1，0） （D）（1，－1）
6、直线
经过
和
,则
与
的大小关系是 （ ）
A. 
B.
C.
D.无法确定
7、无论
为何值,直线
与
的交点不可能在 （ ）
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8、一辆汽车从江油以40千米/时的速度驶往成都,已知江油与成都相距约160千米,则汽车距成都的距离S(千米)与其行驶的时间
(小时)之间的函数关系是 （ ）
A.
B.
C.
D.
9、 关于函数
的图像，有如下说法：
①.图像过点(0，－2)
②图像与轴的交点是（－2，0） ③从图像知随的增大而增大 ④图像不经过第一象限 ⑤图像是与
平行的直线 ，其中正确说法有（ ）
A．5个 B. 4个 C. 3个 D. 2个
10、已知某函数
中，函数值y 随自变量x的增大而减小，那么m取值范围( )
（A） 
(B) 
(C) 
(D) 
二、填空题：本大题共8个小题，每小题3分，共24分.
11、若函数
是正比例函数，则的值是
.
12、将直线
的图象向下平移3个单位长度，得到直线____________.
13、对于一次函数
，当_______时，图象在轴下方.
14、直线
与直线
相交于轴，且与直线
平行，则直线的解析式
为____________.
15．正比例函数
（k≠0）过点（－2，3），则正比例函数表达式为________, 
。
16、直线
与x轴的交点坐标为 ，与 y轴的交点坐标为
17、若直线
和直线
的交点坐标为（m，8）．则m＝ ，b＝ ；
18、某商店出售一种瓜子，其售价（元）与瓜子质量（千克）之间的关系如下表
| 质量 | 1 | 2 | 3 | 4 | …… |
| 售价 | 3.60+0.20 | 7.20+0.20 | 10.80+0.20 | 14.40+0.2 | …… |
由上表得与之间的关系式是 .
三、解答题：本大题共6个小题，共46分. 解答应写出文字说明、证明过程或演算步骤.
19、已知：与
成正比例，且
时，
。
（1）求与之间的函数关系式；
（2）点
在这个函数的图像上，求
的值。（6分）
20、(本小题8分) 已知函数
(1)若函数的图象是经过原点的直线, 求的值.(2分)
(2)若这个函数是一次函数,且随着的增大而减小, 求的取值范围.(3分)
(3)若这个函数是一次函数,且图象不经过第四象限,
求的取值范围.(3分)
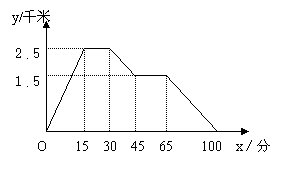21(5分)下图反映的是：小明从家里跑步到小强家，在小强家休息一会儿后，小明与小强一起走到文具店买文具，然后回到家里，其中x表示时间，y表示小明离家的距离。根据图象回答：
（1） 小强家离小明家_______千米，
（2） 小明从家到小强家用_______分；
（3） 文具店离小强家________千米,
（4） 小明从小强家到文具店家用了________分；
（5） 小明从文具店回到家里的平均
速度是__________千米/分。
22、 我市移动通信公司开设了两种通信业务：“全球通”使用者先缴50远基础费，然后每通话1分钟，再付电话费0.4元; “神州行”不缴月基础费,通话1分钟,付电话费0.6元(这里均指市内通话)。若一个月通话x分钟，两种通信方式的费用分别为元和元。（9分）
（1）写出、与之间的函数关系式；
（2）若一个月通话200分钟，选择哪种通信方式较合算？
（3）若某人预计一个月内使用话费200元，则应选择哪种通信方式较合算？
23、(本小题8分) 已知正比例函数与一次函数
相交于点
.问在轴上是否存在一点
，使
.若存在，求出点坐标；若不存在，请说明理由.
24. （10分）某饮料厂为了开发新产品，用A、B两种果汁原料各19千克、17.2千克，试制甲、乙两种新型饮料共50千克，下表是试验的相关数据：
| 饮料 每千克含量 | 甲 | 乙 |
| A（单位：千克） | 0.5 | 0.2 |
| B（单位：千克） | 0.3 | 0.4 |
（1）假设甲种饮料需配制x千克，请你写出满足题意的不等式组，并求出其解集.
（2）设甲种饮料每千克成本为4元，乙种饮料每千克成本为3元，这两种饮料的成本总额为y元，请写出y与x的函数表达式.并根据（1）的运算结果，确定当甲种饮料配制多少千克时，甲、乙两种饮料的成本总额最少，最少成本是多少？