八年级(上)数学半期考试卷
(完卷时间:120分钟 满分:100分)
班级_________姓名_________学号_________成绩_________
(亲爱的同学,这份试卷将再次记录你的自信、沉着、智慧和收获. 请认真审题,看清要求,仔细答题,要相信我能行。)
一、认认真真选,沉着应战!(每小题3分,共30分)
1.下列点一定在函数y=![]() 的图象上的是 ( )
的图象上的是 ( )
A.(-2,2) B.(1,-1) C.(-1,-1) D.(0,0)
2.我校八(8)班男女生人数之比是3∶2,则制作扇形统计图时女生对应的扇形的圆心角是( )
A.144° B.216° C.72° D.108°
3. 下列各条件中,不能作出唯一三角形的是( )
A.已知两边和夹角 B.已知两角和夹边
C.已知两边和其中一边的对角 D.已知三边
4.一次函数![]() 的图象经过( )
的图象经过( )
A.第一、三、四象限 B.第二、三、四象限
C.第一、二、三象限 D.第一、二、四象限
 5.如图,已知
5.如图,已知![]() ,
,![]() ,下列条件中不能判定⊿
,下列条件中不能判定⊿![]() ≌⊿
≌⊿![]() 的是( )
的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() ∥
∥![]()
6.现有一组数据,最大值为93,最小值为22,现要把它分成6组,则下列组距中,合适的为( )
A.9 B.12 C.15 D.18
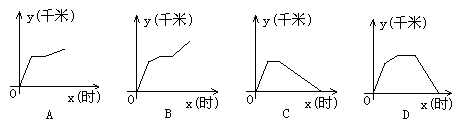 |
7.一天,张老师从学校坐车去开会,由于途中塞车,他只好步行赶到会场,开完会后,他直接回到学校,下图中能体现他离学校的距离y(千米)与时间x(时)的关系的图象是( )
8.已知在一个样本中,50个数据分别落在5个小组内,第一、二、三、五组数据分别为2,8,15,5,则第四小组的频数和频率分别为( )
A.25,50 % B.20,50% C.20,40% D.25,40%
 9.右图中两条直线
9.右图中两条直线![]() 和
和![]() 和交点坐标
和交点坐标
可以看作下列方程组中( )的解。
A.![]() B.
B.![]()
![]()
 C.
C.![]() D.
D.![]()
10.如图,将⊿ADE绕正方形ABCD的顶点A顺时针旋转90度,
得到⊿ABF,连结EF,则下列结论错误的是( )
A.⊿ADE≌⊿ABF B.AE⊥AF
C.∠AEF=45° D.四边形AECF的周长等于ABCD的周长。
二、仔仔细细填,记录自信!(每小题3分,共15分)
 11. 函数
11. 函数![]() 的自变量x的取值范围是
.
的自变量x的取值范围是
.
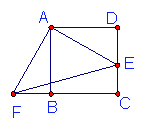
12.如图,要测量河两岸相对的两点A,B的距离,
在AB的垂线BF上取两点C,D,使BC=CD,
再定出BF的垂线DE,使A,C,E在一条直线上,
这时测得DE=16米,则AB= 米。
13.在“线段、锐角、三角形、等边三角形”这四个图形中,是轴对称图形的有 个,其中对称轴最多的是 .线段的对称轴是
 14. 如图,
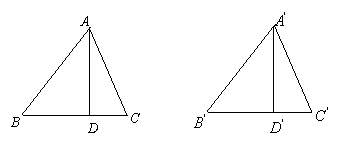
14. 如图,![]() 分别是锐角三角形
分别是锐角三角形![]() 和锐角三角形
和锐角三角形![]() 中
中![]() 边上的高,且
边上的高,且![]() .若使
.若使![]() ,请你补充条件___________.(填写一个你认为适当的条件即可)
,请你补充条件___________.(填写一个你认为适当的条件即可)
15.已知直线![]() 和
和![]() 的交点在第一象限,请写出满足条件的b的值为____________(只写一个即可)
的交点在第一象限,请写出满足条件的b的值为____________(只写一个即可)
三、平心静气做,展示智慧!(共47分)
16. (4分) 如图,要在S区建一个集贸市场,使它到公路,铁路距离相等,离公路与铁路交叉处600米。这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20 000)。
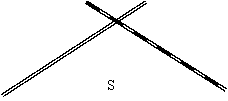
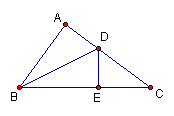
17.(4分)如图,在△ABC中,AD=DE,AB=BE,∠A=80°,求∠CED的度数
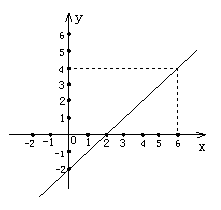
18.(6分)一次函数的图象如图所示:
(1)求出该一次函数的关系式.
(2)当x=10时,y的值是多少?
(3)当y=12时,x的值是多少?
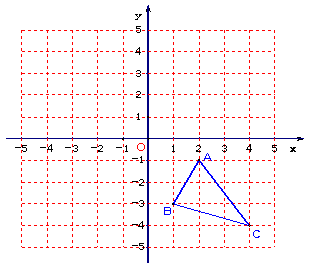
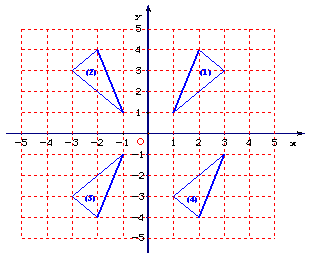 19. (5分)(1)如图所示编号为①、②、③、④的四个三角形中,关于y轴对称的两个三角形的编号为 ;(2)在图4中,画出与△ABC关于x轴对称的△A1B1C1
19. (5分)(1)如图所示编号为①、②、③、④的四个三角形中,关于y轴对称的两个三角形的编号为 ;(2)在图4中,画出与△ABC关于x轴对称的△A1B1C1
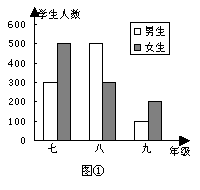
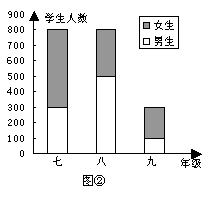
20.(本题满分6分)图①、②是李晓同学根据所在学校三个年级男女生人数画出的两幅条形图.
(1)两个图中哪个能更好地反映学校每个年级学生的总人数?
哪个图能更好地比较每个年级男女生的人数?
(2)请按该校各年级学生人数在图③中画出扇形统计图.
 |  | ||
21.(7分)某人从A城出发,前往离A城30千米的B城。现在有三种车供他选择:①自行车,其速度为15千米/时;②三轮车,其速度为10千米/时;③摩托车,其速度为40千米/小时。
(1)用什么车能使他从A城到达B城的时间小于2小时,请说明理由。
(2)设此人在行进途中离A城的路程为s千米,行进时间为t小时,就(1)所选定的方案,试写出s与t的函数关系式(注明自变量t的取值范围)。并在平面直角坐标系中画出此函数的图像。
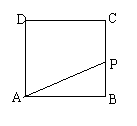 22.(7分)如图,在边长为2的正方形ABCD的一边BC上,一点P从B点运动到C点,设BP=x,四边形APCD的面积为y.
22.(7分)如图,在边长为2的正方形ABCD的一边BC上,一点P从B点运动到C点,设BP=x,四边形APCD的面积为y.
⑴ 写出y与x之间的函数关系式及x的取值范围;
⑵ 说明是否存在点P,使四边形APCD的面积为1.5?
23.(8分)如图11,A、B两点分别位于一个池塘的两侧,池塘西边有一座假山D,在DB的中点C处有一个雕塑,张倩从点A出发,沿直线AC一直向前经过点C走到点E,并使CE=CA,然后她测量点E到假山D的距离,则DE的长度就是A、B两点之间的距离.
(1)你能说明张倩这样做的根据吗?
(2)如果张倩恰好未带测量工具,但是知道A和假山、雕塑分别相距200米、120米,你能帮助她确定AB的长度范围吗?
(3)在第(2)问的启发下,你能“已知三角形的一边和另一边上的中线,求第三边的范围吗?”请你解决下列问题:在△ABC中,AD是BC边的中线,AD=3cm,AB=5cm,求AC的取值范围.
四、发散思维,游刃有余!(共8分)
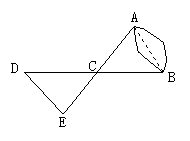
24. (1)如图1,以![]() 的边
的边![]() 、
、![]() 为边分别向外作正方形
为边分别向外作正方形![]() 和正方形
和正方形![]() ,连结
,连结![]() ,试判断
,试判断![]() 与
与![]() 面积之间的关系,并说明理由.
面积之间的关系,并说明理由.
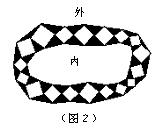
(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石
铺成.已知中间的所有正方形的面积之和是![]() 平方米,内圈的所有三角形的面积之和
平方米,内圈的所有三角形的面积之和
是![]() 平方米,这条小路一共占地多少平方米?
平方米,这条小路一共占地多少平方米?
 |
 |
友情提示:抓紧时间,检查一遍!!!