八年级(上)数学期中复习练习(3)--第三章
班级 姓名 得分
一、填空题（36分）
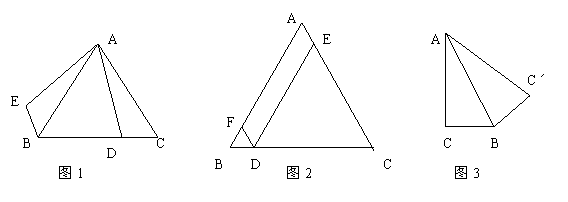
1、如图1，△ABC是等边三角形，D是BC上一点，△ABE是△ACD经过旋转形成的.则
（1）旋转中心是 ，旋转角是 度；
（2）连接DE，则△ADE的形状是 ；
（3）请在图中画出AC的中点M以及M点经过上述旋转后的对应点N.
 |
2、下列图形中：（1）线段；（2）等腰三角形；（3）等腰梯形（4）平行四边形；（5）矩形；（6）菱形；（7）正方形；（8）圆，既是轴对称图形又是中心对称图形的有
（填写序号）.
3、已知在
ABCD中，AB=14
，BC=16，则此平行四边形的周长为
.
4、矩形的两条对角线的夹角为
，较短的边长为12，则对角线长为 .
5、已知菱形的两条对角线长为8和6，则
（1）该菱形的周长为
；（2）该菱形的面积为
.
6、已知菱形的周长为24，其中一条对角线的长为6，那么它的另一条对角线的长为
，较大的内角是 °，较长的对角线与该菱形的边的夹角为 °.
二、选择题（20分）
1、四边形ABCD中，AC与BD相交于点O，如果只有条件“AB∥CD”，那么还不能判定四边形ABCD为平行四边形.给出以下四种说法：
（1）如果再加上条件“BC=AD”，那么四边形ABCD一定是平行四边形；
（2）如果再加上条件“∠BAD=∠BCD”，那么四边形ABCD一定是平行四边形；
（3）如果再加上条件“AO=OC”，那么四边形ABCD一定是平行四边形；
（4）如果再加上条件“∠DBA=∠CAB”，那么四边形ABCD一定是平行四边形.
其中正确的说法是（ ）
A、（1）（2） B、（1）（3）（4） C、（2）（3） D、（2）（3）（4）
2、有下列说法：①四个角都相等的四边形是矩形；②有一组对边平行，有两个角为直角的四边形是矩形；③两组对边分别相等且有一个角为直角的四边形是矩形；④对角线相等且有一个角是直角的四边形是矩形；⑤对角线互相平分且相等的四边形是矩形；⑥一组对边平行，另一组对边相等且有一角为直角的四边形是矩形.
其中，正确的个数是（ ）
A、2个 B、3个 C、4个 D、5个
3、不能判定一个四边形是菱形的条件是（ ）
A、对角线互相平分且有一组邻边相等 B、四边相等
C、两组对角相等，且一条对角线平分一组对角 D、对角线互相垂直
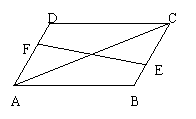
4、如图2，在ΔABC中，AB=AC=5，D是BC上的点，DE∥AB交AC于点E，DF∥AC交AB于点F，那么四边形AFDE的周长是 （ ）
A、5 B、10 C、15 D、20
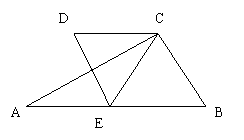
5、如图3，把三边BC=3，AC=4，AB=5的三角形AB翻折成ΔABCˊ，则CCˊ长为（ ）
A、
B、
C、
D、
三、解答题
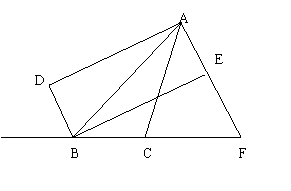
1、如图，ABCD中，BE=DF.试说明AC、EF互相平分.（8分）
2、如图，已知AB∥CD，∠ACB=90°，E为AB的中点，CE=CD，DE与AC相交于F点.
则DE、AC有怎样的关系？说明你的理由.（10分）
 |
3、如图，BE、BD是ΔABC中∠ABC的内、外角平分线，AD⊥BD于点D，AE⊥BE于点E，交BC的延长线于点F.则DE与BF相等吗？为什么？（10分）
 |
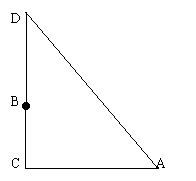
4、如图，在一棵树的10米高的B处有两只猴子，其中一只猴子沿树爬下，走到离树20米处的池塘A处 ，另一只爬到树顶D处直跃池塘的A处，如果两只猴子所经过的路程相等，则这棵树有多高（设树与地面垂直）？（10分）
 |
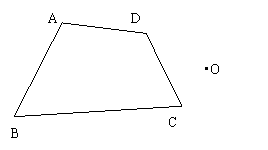四、作图题：作出四边形ABCD关于O点成中心对称的四边形AˊBˊCˊDˊ（6分）