八年级（上）第二次了解性测试
数 学 试 卷
（总分120分 答卷时间100分钟）
一、选择题（本题共10小题；每小题3分，共30分）
1、反映某种股票的涨跌情况，应选择 【 】
A．条形统计图 B．折线统计图 C．扇形统计图 D．直方图
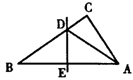
2、如图，△ABC中边AB的垂直平分线分别交BC、AB于点D、E，AE=3cm，△ADC的周长为9cm，则△ABC的周长 【 】
A．10cm B．12cm C．15cm D．17cm
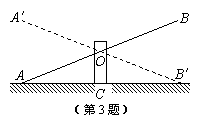3、如图是跷跷板的示意图，支柱OC与地面垂直，点O
是横板AB的中点，AB可以绕着点O上下转动，当A
端落地时，∠OAC=20°，横板上下可转动的最大角度
（即∠A′OA）是 【 】
A．80° B．60° C．40° D．20°
4、 一个容量为80的样本中，最大值是141，最小值是50，取组距为10，则这个样本可以成【 】
A．10组 B．9组 C．8组 D．7组
5、下列命题中，不正确的是 【 】
A．关于直线对称的两个三角形一定全等
B．角是轴对称图形
C．等边三角形有3条对称轴
D．等腰三角形一边上的高、中线及这边所对角的角平分线重合
6、 等腰三角形的一个内角是50°，则这个三角形的底角的大小是 【 】
A．65°或50° B．80°或40° C．65°或80° D．50°或80°
7、使两个直角三角形全等的条件是 【 】
A．一锐角对应相等 B．两锐角对应相等
C．一条边对应相等 D．两条直角边对应相等
8 、直线
关于
轴对称的直线的解析式为
【 】
A．
B．
C．
D．
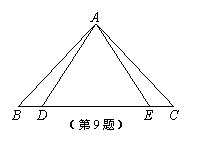
9、 如图，AB=AC，AD=AE，∠B=50°，∠AEC=120°，
则∠DAC的度数等于 【 】
A．120° B．70°
C．60° D．50°
10、如图，将⊿ADE绕正方形ABCD的顶点A顺时针旋转90度，
得到⊿ABF，连结EF，则下列结论错误的是（ ）
A.⊿ADE≌⊿ABF B.AE⊥AF
C.∠AEF=45° D.四边形AECF的周长等于ABCD的周长。
二、填空题（每小题3分，共30分）
11、直线y=kx+2过点（-1，0），则k的值是_________
12、等腰三角形的腰长是6，则底边长3，周长为____________.
13、在一幅扇形统计图中，扇形表示的部分占总体的百分比为20％，则此扇形的圆心角为 °．
14、已知一次函数
，请你补充一个条件__________，使函数图象经过第二、三、四象限．
15、已知在一个样本中有50个数据，它们分别落在5个组内，第一、二、三、四、五组数据的个数分别为2，8，15，x，5，则x等于______，第四组的频率为_________．
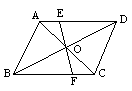
16、如图，AB∥CD，AD∥BC，OE=OF，则图中全等三角形有______组.
|
cm，AB=_________cm．
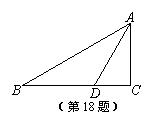
18、如图，在△ABC中，∠C=90°，AD平分∠BAC，BC=10cm，
BD=7cm，则点D到AB的距离为_____________cm．
19、在平面直角坐标系
中，已知点A（2，－2），在坐标轴上
确定点P，使△AOP为等腰三角形，则符合条件的有_______个．
20、当m= _______时，函数y=(m-3)x2m+1+4x-3是一次函数.
三、解答题（本题共8题；共60分）
21、（5分）作图题（不写作图步骤，保留作图痕迹）．
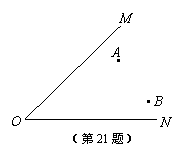已知：如图，求作点P，使点P到A、B两点的距离相等，且P到∠MON两 边 的距离也相等．
22、(9分)已知一次函数y=kx+b的图象经过（3，5）和（－4，－9）两点．
（1）求这个一次函数的解析式；
（2）画出这个一次函数的图象；
（3）若点（a，2）在这个函数图象上，求a的值．
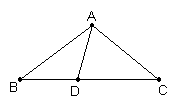23、(6分）已知，如图ΔABC中，AB＝AC,D点在BC上，且BD＝AD，DC＝AC.将图中的等腰三角形全都写出来.并求∠B的度数.
24、(6分）如图，AD⊥BC于D，AD=BD，AC=BE。请猜想说明∠BED和∠C有何特殊关系？
 |
25、(6分)如图，已知P点是∠AOB平分线上一点，PC⊥OA，PD⊥OB，垂足为C、D，
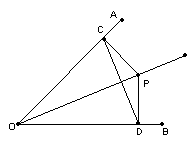（1）∠PCD=∠PDC吗？ 为什么？
（2）OP是CD的垂直平分线吗？ 为什么？
26、（9分）金鹰集团对应聘者甲、乙、丙进行面试，并从专业知识、工作经验、仪表形象三方面给应聘者打分，每一方面满分20分，最后的打分制成条形统计图（如图）．
（1）利用图中提供的信息，回答下列问题：在专业知识方面3人得分谁是最过硬的？在工作经验方面3人得分谁是最丰富的？在仪表形象方面谁最有优势？
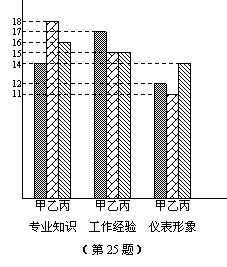（2）如果专业知识、工作经验、仪表形象三个方面的重要性之比为10∶7∶3，那么作为人事主管，你应该录用哪一位应聘者？为什么？
（3）在（2）的条件下，你对落聘者有何建议？
27、（9分）某市的A县和B县春季育苗，急需化肥分别为90吨和60吨，该市的C县和
D县分别储存化肥100吨和50吨，全部调配给A县和B县，已知C、D两县
运化肥到A、B两县的运费（元/吨）如下表所示．
|
| C | D |
| A | 35 | 40 |
| B | 30 | 45 |
（1）设C县运到A县的化肥为x吨，求总运费W（元）与x（吨）的函数解析式，并写出自变量x的取值范围；
（2）求最低总运费，并说明总运费最低时的运送方案．
28、（10分）如图，直线y=kx+6分别与x轴、y轴相交于点E和点F，点E的坐标为 （-8，0），点A的坐标为（-6，0）。
（1）求k的值；
（2）若点P（x，y）是第二象限内的直线上的一个动点，当点P运动过程中，试写出 △OPA的面积S与x的函数关系式，并写出自变量x的取值范围；
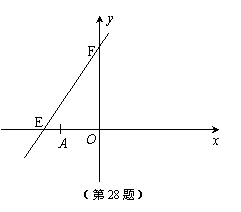（3）探究：当P运动到什么位置时，△OPA的面积为
，并说明理由。