八年级上学期秋第一次月测
(时间：120分钟，满分120分)
一、填空题（每题3分，共30分）
1、在圆的周长公式C=2
R中，常量是 ，变量是 ，C是 的函数。
2、函数
的自变量
的取值范围是
，当
时，
。
3、三角形的周长是
，三边长分别是
、
、
，则
与的函数关系式为
，自变量的取值范围是 。
4、当
时，函数
是一次函数。当 时，函数
是正比例函数。
5、一次函数
的图象不经过第 象限，随的增大而 。
6、一次函数
的图象是
，它由 个点组成的，因此说方程
的解有
个。
7、一次函数
与
的图象是两条
的直线，因此方程组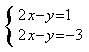
的解的情况是
。
8、一次函数的图象经过点
与
，它的解析式是
。
9、将直线
向上平移5个单位，得到直线
；将直线
向下平移5个单位，得到直线
。
10、直线
与轴的交点坐标为
，与轴的交点坐标为
，这条直线与坐标轴围成的三角形面积为
。
二、选择题（每题3分，共24分）
1、下列函数：①
②
③
④ 
中，一次函数的个娄是（ ）
A、4； B、3； C、2； D、1。
2、已知一次函数
，若随的增大而减小，则该函数的图象经过
（ ）
A、第一、二、三象限 B、第一、二、四象限
C、二、三、四象限 D、一、三、四象限
3、点
（
，
），
（
，
）是一次函数
图象上的两个点，且
，则与的大小关系是
（ ）
A．
B。
C．
D．
4、已知函数
是一次函数，则
的值是
（ ）
A．2
B．
C．
D．
5、若正比例函数
的图象经过点
和点
，当时，,则的取值范围是
( )
A．
B．
C．
D．
6、已知一次函数
的图象不经过第二象限，则
（ ）
A．
B．
C．
D．
7、一次函数满足
时，
，
时，
，则一次函数的解析式为（ ）
A．
B． C．
D．
8、已知一次函数
和
的图象都经过点
，且与轴分别交于
两点，那么
的面积是
（ ）
A．2 B．3 C．4 D．5
三、解答题（共66分）
1、根据下列条件分别确定函数的解析式（12分）
（1）与成正比例，
时
（2）直线经过点
与
2、已知
与
成正比例，且时
，
时，求与之间函数关系式。（12分）
3、已知等腰三角形的顶角为，底角为。（12分）
（）写出底角与顶角之间的函数关系式（为自变量）
（）写出自变量的取值范围。
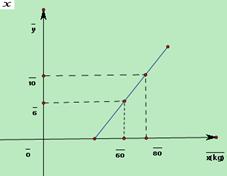
4、某地长途汽车公司规定旅客可随身携带一定质量的行李，如果超过规定，则需要购买行李票，行李票费用
是行李质量
的一次函数，其图象如图所示（15分）
求：（1）与之间的函数关系式。
（2）旅客最多可免费携带行李的千克数
5、某车间有20名工人，每人每天加工甲种零件5个或4个。在这20名工人中，派名工人加工甲种零件，其余的加工乙种零件，已知每加工一个甲种零件可获利16元，每加工一个乙种零件可获利24元。（15分）
（1）写出此车间每天所获利
与
之间的函数关系式。
（2）若要使车间每天获利不低于1800元，则至少要派多少史工人加工乙种零件？