![]() 八年级上学期数学期末模拟试卷
八年级上学期数学期末模拟试卷
(考试时间:100分钟 总分:100分)
一.选择题:(本题共10小题;每小题2分,共20分)
1.下列计算正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.下列四点中,在函数![]() 的图象上的点是 ( )
的图象上的点是 ( )
A.(-1,1) B.(-1,-1) C.(2,0) D.(0,-1.5)
3.下面有四个汽车标致图案,其中是轴对称图形的是( )
A、②③④ B、①②③ C、①②④ D、①②④
 ①
②
③
④
①
②
③
④
4.函数![]() 中自变量
中自变量![]() 的取值范围是( ).
的取值范围是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
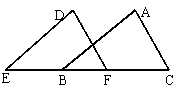 5.如图,
5.如图,![]() 四点在一条直线上,
四点在一条直线上,![]() 再添一个条件仍不能证明⊿ABC≌⊿DEF的是( )
再添一个条件仍不能证明⊿ABC≌⊿DEF的是( )
A.AB=DE B..DF//AC
C.∠E=∠ABC D.AB//DE
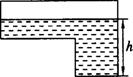
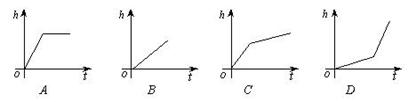
6.如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的注水,下面能大致表示水的最大深度h与时间t之间的关系的图像是( ) .
7.等腰三角形的周长为
A.
 8.某校九(3)班的全体同学喜欢的球类运动用图所示扇形统计图来表示,下面说法正确的是( )
8.某校九(3)班的全体同学喜欢的球类运动用图所示扇形统计图来表示,下面说法正确的是( )
A.从图中可以直接看出喜欢各种球类的具体人数
B.从图中可以直接看出全班的总人数
C.从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况
D.从图中可以直接看出全班同学现在喜欢各种球类的人数的大小关系
5.如图,已知![]() ,
,![]() ,增加下列条件:①
,增加下列条件:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中能使
.其中能使![]() 的条件有( )
的条件有( )
(A)![]() 个 (B)
个 (B)![]() 个 (C)
个 (C)![]() 个 (D)
个 (D)![]()
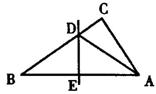
10.如图,![]() 中边
中边![]() 的垂直平分线分别交
的垂直平分线分别交![]() 于点
于点![]() ,
,![]() 的周长为
的周长为![]() ,则
,则![]() 的周长是( )
的周长是( )
 A.
A.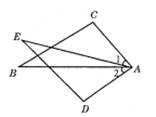
第9题 第10题
二、填空题:(本题共6小题,每题3分,共18分)
11.某种大米的单价是2.4元/千克,当购买X千克大米时花费为Y元,则X与Y的函数关系式_________.。
12.要使一次函数![]() 的图像经过第一、三、四象限,则
的图像经过第一、三、四象限,则![]() 的取值范围是__________。
的取值范围是__________。
13.生活垃圾中,直接填埋的占23%,焚烧的占73%,回收利用的占4%,要反映这个问题中的数据,你认为最适宜的统计图是____________。
14.50个数据分别落在5个组内,其中第一组有6个数据,则该组的百分率是_________;第二小组的百分率为0.1,则该组内数据的个数是_________。
15.等腰三角形底边长为
16.已知![]() ,
,![]() ,则
,则![]() =__________,
=__________,![]()
三、解下列各题:(本题共3小题,共17分)
17.分解因式(每小题4分,共8分)
(1)![]() (2)
(2)![]()
18.(本题4分)计算![]()
19.(本题5分)先化简再求值:![]() ,其中
,其中![]() =5,y=2。
=5,y=2。
四、解下列各题:(本题共3小题,共17分)
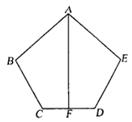
20.(本题5分)已知:如图,![]() 且
且![]() 是
是![]() 的中点,求证:
的中点,求证:![]()
 |
21(本题6分)某校学生会在“暑假社会实践”活动中组织学生进行了社会调查,并组织了评委会对学生写出的调查报告进行了评比。学生会随机抽查了部分统计,绘制了统计图,请根据图回答下列问题:
①学生会共抽取了 份调查报告。
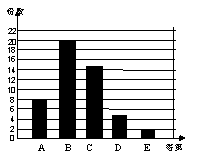 ②若E等为优秀,则优秀率
。
②若E等为优秀,则优秀率
。
③学生会共收到调查报告1000份,请估计该校有多少份调查报告的等第为E ?
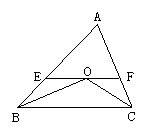
22.(本题6分)如图所示,在![]() 中,
中,![]() 的平分线交于点O,过点O作
的平分线交于点O,过点O作![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,试求
,试求![]() 的值
的值
五、(本题共2小题,共12分)
23.(本题6分)2003年我国遭受到“非典”灾难,全国人民万众一心,众志成城,抗击“非典”。图A-1是我市某中学“献爱心,抗非典”自愿捐款活动中,学生捐款情况的条形图(纵轴数据为人均捐款数目),图A-2是该校学生人数比例分布图,该校共有学生1450人。
①初三学生共捐款多少元 ?
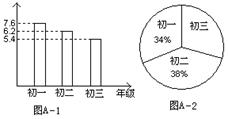 ②该校学生共捐款多少元?
②该校学生共捐款多少元?
③平均每个学生捐款多少元?
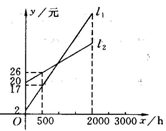
24.(本题6分)如图所示,![]() 分别表示一种白灯和节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间
分别表示一种白灯和节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间![]() 的函数关系图象,假设两种灯的使用寿命都是
的函数关系图象,假设两种灯的使用寿命都是![]() ,照明的效果一样。
,照明的效果一样。
①根据图象分别求出![]() 的函数关系式
的函数关系式
②当照明时间为多少时,两种灯的费用相等
③小亮房间计划照明![]() ,他买了一个白灯和一个节能灯,请你帮他设计最省钱的用灯方法。
,他买了一个白灯和一个节能灯,请你帮他设计最省钱的用灯方法。
六、(本题共2小题,共16分)
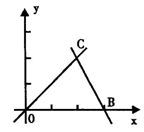 25.(本题)如图,直线
25.(本题)如图,直线![]() 的函数关系式分别
的函数关系式分别![]() ,动点
,动点 ![]() (
(![]() ,0)在
,0)在![]() 上运动(0<
上运动(0<![]() <3),过点
<3),过点![]() 作直线
作直线![]() 与
与![]() 轴垂直。
轴垂直。
(1)求点![]() 的坐标,并回答当
的坐标,并回答当![]() 取何值时
取何值时![]() >
>![]() ?
?
(2)设![]() 中位于直线
中位于直线![]() 左侧部分的面积为
左侧部分的面积为![]() ,求出
,求出![]() 与
与![]() 之间函数关系式.
之间函数关系式.
(3)当![]() 为何值时,直线
为何值时,直线![]() 平分
平分![]() 的面?
的面?
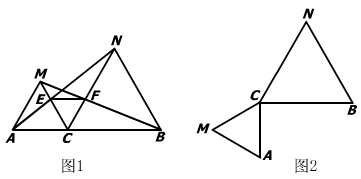
26.(本题8分)已知:如图1,点C为线段AB上一点,△ACM,△CBN都是等边三角形,AN交MC于点E,BM交CN于点F.
(1).求证:AN=BM;
(2).求证:△CEF为等边三角形;
(3).将△ACM绕点C按逆时针方向旋转900,其他条件不变,在图2中补出符合要求的图形,并判断第(1)、(2)两小题的结论是否仍然成立(不要求证明)
 |