整式章测试

第十五章整式章测试

一、选择题：本题共6题，每题3分，共18分。

1．下列各单项式中，与2x⁴y是同类项的为（　　）

A.2x⁴　　　 B.2xy　　　　C.x⁴y　　　　D.2x²y³

2．(x－a)(x²＋ax＋a²)的计算结果是（　　）

A.x³＋2ax²－a³　 B.x³－a³　 C.x³＋2a²x－a³　D.x²＋2ax²＋2a²－a³

3．下面是某同学在一次测验中的计算摘录：

①3a＋2b＝5ab； ②4m³n－5mn³＝－m³n； ③3x³·(－2x²)=－6x⁵；

④4a³b÷(－2a²b)＝－2a； ⑤(a³)²＝a⁵； ⑥(－a)³÷(－a)＝－a²

其中正确的个数有（　  ）

A.1个　　　 B.2个　　　 C.3个　　　　D.4个　　

4．小亮从一列火车的第m节车厢数起，一直数到第2m节车厢，他数过的车厢节数是………………（　　）

A.m＋2m＝3m　　　　　　　 　B.2m－m＝m　

　 C.2m－m－1＝m－1　　　　　　D.2m－m＋1＝m＋1

5．下列分解因式正确的是（　　）

A.x³－x＝x(x²－1)　　　　　　 B.m²＋m－6＝(m＋3)(m－2)　

C.(a＋4)(a－4)＝a²－16　　　 D.x²－y²＝(x－y)(x＋y)

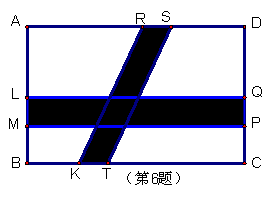
6．如图：矩形花园中ABCD，AB＝a，AD＝b，花园中建有一条矩形道路LMPQ及一条平行四边形道路RSTK。若LM＝RS＝c，则花园中可绿化部分的面积为（　　）

A.bc－ab＋ac＋b²　　　　　  B.a²＋ab＋bc－ac　

C.ab－bc－ac＋c²　　　 　　 D.b²－bc＋a²－ab

二、填空题（每小题4分，共28分）

7．(1)当x_______时，(x－4)⁰等于______；

(2)( )²⁰⁰²×(1.5)²⁰⁰³÷(－1)²⁰⁰⁴＝________。

8．分解因式：a²－1＋b²－2ab＝­­­________________.

9．如图，要给这个长、宽、高分别为x、y、z的箱子打包，其打包方式如图所示，则打包带的长至少要　　　　　　　 （单位：mm）（用含x、y、z的代数式表示）。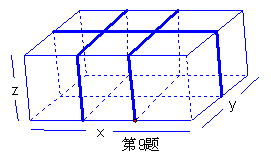

10．如果（2a＋2b＋1）(2a＋2b－1)=63，那么a＋b的值为　　　　　  。

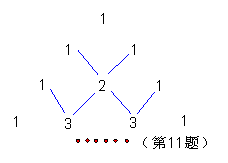
11．下表为杨辉三角系数表的一部分，它的作用是指导读者按规律写出形如(a＋b)ⁿ(n为正整数)展开式的系数，请你仔细观察下表中的规律，填出(a＋b)ⁿ展开式中所缺的系数. (a＋b)=a＋b 

(a＋b)²=a²＋2ab＋b²

(a＋b)³=a³＋3ab＋3ab＋b³

则(a＋b)⁴=a⁴＋　　a³b＋　　a²b²＋　　ab³＋b⁴

12．某些植物发芽有这样一种规律：当年所发新芽第二年不发芽，老芽在以后每年都发芽。发芽规律见下表（设第一年前的新芽数为a）照这样下去，第8年老芽数与总芽数的比值为　　　　　 （精确到0.001）

第×年	1	2	3	4	5	…
老芽数	a	a	2a	3a	5a	…
新芽数	0	a	a	2a	3a	…
总芽数	a	2a	3a	5a	8a	…

13．某体育馆用大小相同的长方形木板镶嵌场面，第1次铺2块，如图（1）；第2次把第1次铺的完全围起来，如图（2）；第3次把第2次铺的完全围起来，如图（3）；…。依此方法，第n次铺完后，用字母n表示第n次镶嵌所使用的木板数　　　　　

 

 

 

三、解答题材

14．(10分)计算：[x(x²y²－xy)－y(x²－x³y)]÷3x²y

15．(18分)已知：m²＝n＋2，n²＝m＋2(m≠n)，求：m³－2mn＋n³的值。

16．（18分）某商店积压了100件某种商品，为使这批货物尽快脱手，该商店采取了如下销售方案，将价格提高到原来的2.5倍，再作3次降低处理；第一次降价30%，标出“亏本价”；第二次降价30%，标出“破产价”；第三次降价30%，标出“跳楼价”。3次降价处理销售结果如下表：

降价次数	一	二	三
销售件数	10	40	一枪而光

（1）跳楼价占原来的百分比是多少？

（2）该商品按新销售方案销售，相比原价全部售完，哪种方案更盈利