第三章 中心对称图形（一）
一、本章知识结构：
图形的旋转
中心对称及性质设计中心对称图案
三解形和梯形的中位线
二、练习
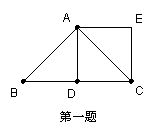
1．如图，△ABC是等腰直角三角形，D是斜边BC上的中点，△ABD绕点A旋转到△ACE的位置，恰与△ACD组成正方形ADCE，则△ABD按 时针方向旋转了 °
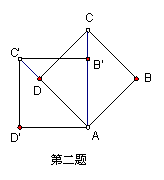
2．如图，正方形ABCD旋转后得到正方形AB′C′D′。
① 旋转中心是 ② 旋转角是 ③ 若AB=1，则C′D=
3．线段是轴对称图形，也是
对称图形，它的对称中心是
；当点A、B、O满足条件OA=OB且
时，点A、B关于点O成中心对称，反过来，若点A、B关于点O成中心对称，则A、B、O三点共线且
 | |||
 | |||
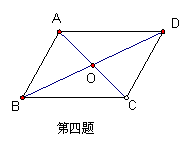
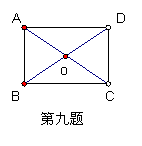
4．如图，四边形ABCD是平行四边形，对角线AC、BD相交于点O，已知AB=25，BC=30，AC=28，BD=46，∠ABC=70°。则AD= ，CD= ，∠ADC= ，∠BCD= ，△COD的周长= 。
5．如果□ABCD的周长为32
，且AB=6，那么BC= ，CD=
，DA=
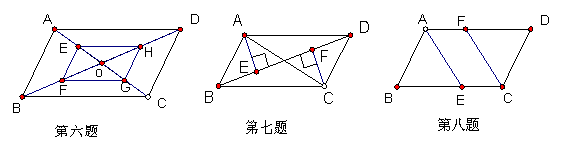
6．如图，□ABCD的对角线相交于点O，E、F、G、H分别是OA、OB、OC、OD的中点，则四边形EFGH ，理由是
7．如图，在□ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F，四边形AECF是平行四边形吗？为什么？
8．如图，在□ABCD中，∠BAD、∠BCD的平分线分别交BC、AD于点E、F，四边形AECF是平行四边形吗？为什么？
9．如图，在矩形ABCD中，对角线AC、BD相交于点O，AB=2，AC=4，
① 根据“矩形的对角线
”，可以得到BD=
② 根据“矩形的对角线
”，可以得到AO=BO=
AC=
，又AB=2，所以△AOB是 三角形。
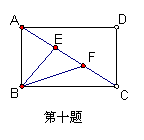
10．如图，在矩形ABCD中，AB=6，BC=8，E、F是AC的三等分点，则△BEF的面积是
。
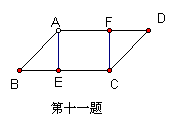
11．如图，在□ABCD中，AE⊥BC，垂足为E，CF⊥AD，垂足为F，则四边形AECF是 四边形。理由是 。
 |  |  | |||
12．如果菱形的边长是3，一条对角线的长也是3，那么菱形的另一条对角线的长是
13．在菱形ABCD中，对角线AC、BD相交于点O，如果AC=8，BD=6，那么AB= ，菱形的周长 =，菱形的面积= 。
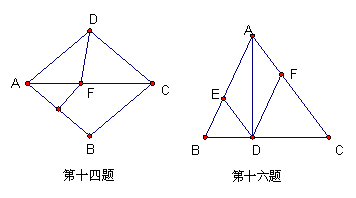
14．如图，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF= 。
15．两张等宽的纸条交叉重叠在一起，重叠的部分ABCD是 形。
16．如图，AD是△ABC的高，DE∥AC，DF∥AB，则△ABC满足条件 时，四边形AEDF是菱形。
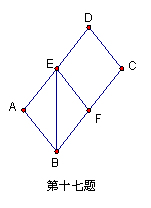17．如图，□ABCD中，AD=2AB，∠ABC的平分线交AD于点E，EF∥AB交BC于点F，则四边形ABFE和四边形EFCD都是
形。
18．□ABCD的四个内角的平分线围成的四边形是 形。
19．一个矩形的两条对角线互相垂直，则这个矩形是 。
20．一个菱形的两条对角线相等，这个菱形也是 。
21．如果△ABC的三条中位线分别为3，4，6，那么△ABC的周长为
22．如果三角形的周长为10，那么连接各边中点所得的三角形的周长为 。
23．梯形的两底长分别为6和8，则中位线的长是
。若梯形的一底长为6，中位线长为8，则另一底的长为
。
24．一个等腰梯形的周长是80，高是12，并且腰长与中位线长相等，则这个梯形的面积是
。
25．顺次连接任意四边形的中点所得的四边形是 形。
顺次连接矩形的中点所得的四边形是 形。
顺次连接菱形的中点所得的四边形是 形。
顺次连接正方形的中点所得的四边形是 形。
顺次连接等腰梯形的中点所得的四边形是 形。
26．任意一种全等的三角形或四边形可以镶嵌平面，正三角形，正方形，正六边形，长方形可以镶嵌平面。
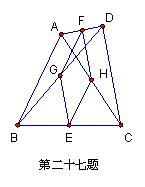27．如图，四边形ABCD中，AB=CD，点E、F、G、H分别是BC、AD、BD、AC的中点，猜想四边形EHFG的形状并说明理由。
 |
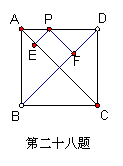28．如图，P是边长为4的正方形ABCD的边AD上的一点，且PE⊥AC，PF⊥BD，则PE+PF=
。
29．一梯形的中位线将梯形分成面积为1：2的两部分，那么上底
、中位线
、下底
的比
=
。
30．以长为5，4，7的三条线段中的两条为边，另一条为了对角线画平行四边形，可以画出形状不同的平行四边形的个数有
个。
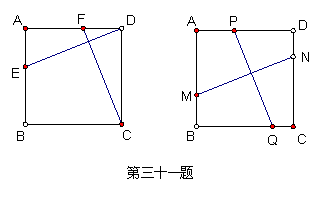
31．如图，在正方形ABCD中。
（1）若点E、F分别在AB、AD上，且AE=DF。试判断DE与CF的数量及位置关系，并说明理由。
（2）若P、Q、M、N是正方形ABCD各边上的点，PQ与MN相交，且PQ=MN，问PQ⊥MN成立吗？为什么？
 |