第十六章 平行四边形检测卷
一、选择题(每题3分，共30分)
1．在
ABCD中，对角线AC和BD相交于点0，则图中面积相等的三角形有( )
A．6对 B．8对 C．10对 D．12对
2．平行四边形的对角线为6和10，则其中一边
的取值范围是( )
A．4<<16 B．2<<8 C．0<<10
D．O<<6
3．平行四边形具有而非平行四边形的图形不具有的性质是( )
A．内角和与外角和都是
B．不稳定性
C．对角线互相平分 D．最多有三个钝角
4．如果矩形的一边与对角线的夹角为
，则两条对角线相交所成的锐角的度数为( )
A．60。 B．70。 C．80。 D．90。
5．梯形ABCD中，AD∥BC，则∠A：∠B：∠C：∠D 的值可能是( )
A．4︰6︰2︰8 B．2︰4︰6︰8
C．4︰2︰8︰6 D．8︰4︰2︰6
6．菱形的一条对角线与它的边相等，则它的锐角等于( )
A．30
B．45 C．60 D．75
7．已知等腰梯形ABCD中，AD∥BC，AB=CD=2cm，BC=5cm，∠A=120，则它的周长为( )
A．16cm B．14cm C．12cm D．10cm
8．菱形ABCD中，AC=10cm，BD=24cm．则菱形的面积为( )
A．30
B．60 C．120 D．240
9．已知平行四边形的一条边长为14，下列各组数中能分别作为它的两条对角线长的是( )
A．10与16 B．12与16 C．20与22 D．10与40
10．同学们曾玩过万花筒，它是由三块等长等宽的玻璃片围成的，如图16—23所示的是万花筒中看到的一个图案，图中所有的小三角形是能重合的等边三角形， 其中菱形AEFG可以看成把
菱形ABCD以点A为中心( )
A．顺时针旋转60得到
B．顺时针旋转120得到
C．逆时针旋转60得到
D．逆时针旋转120得到
二、填空题(每题3分，共30分)
11．如图16—24所示，四边形ABCD为正方形，P为AC上一点，AP=AD，EG上AC于点P，交CD于G，则∠DPG= ．
12．如图16—25所示，四边形ABCD是对角线长为20cm的正方形，EF∥DB，FG∥AC，则EF+FG=
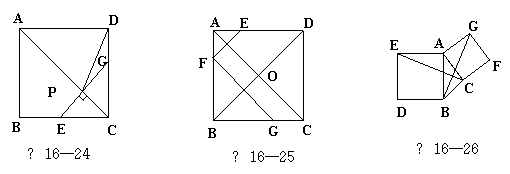
13．如图16—26，以△ABC的边AB、AC为边向三角形外作正方形ABDE及正方形ACFG，则△EAC可以看作 绕点A 得到．
14．梯形的面积为54cm。，两底长的比是4︰5，如果高为6cm，那么梯形两底的长分别等于 ．
15．在直角梯形中，较长的底为10cm，这个底上的高为4cm，一个底角是45。，则此梯形的面积为 ．
16．平行四边形是 对称图形，而不是 对称图形， 是它的对称中心．
17．如图16—27，在平行四边形ABCD中，AE、CF分别是∠BAD和∠BCD的角平分线，根据现有的图形，请添加一个条件，使四边形AECF为菱形，则添加的一个条件可以是 (只需写出一个即可，图中不能再添加别的“点”或“线”)．
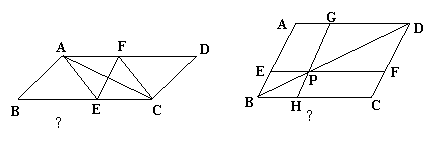
18．如图16—28所示，在ABCD中，EF∥BC，GH∥AB，EF、GH的交点P在BD上，图中有 对四边形面积相等；它们是
19．任意一个平行四边形，当它的一个锐角增大到 度时，就变成了矩形；当它的一组邻边变到 时，就变成了菱形．
20．一张长方形的桌子有四个角，砍去一个角后，还剩下 个角．
三、解答题(每题10分，共40分)
21．阅读下列材料：
当矩形一个角的平分线分矩形一边为lcm和3cm两部分时，则这个矩形的面积为4或12；
当矩形一个角的平分线分矩形一边为lcm和4cm两部分时，则这个矩形的面积为5。或20．
根据以上情况，完成下面填空：
(1)当矩形一个角的平分线分矩形一边为lcm和5cm两部分时，则这个矩形面积为
或
；
(2)当矩形一个角的平分线分矩形一边为lcm和
两部分时，则这个矩形面积为 或
．(n为正整数)
22．已知：ABCD的周长为3.6cm，△ABD的周长为2.8cm，过点D引直线AB的垂线，垂足恰为线段AB的中点，求ABCD的边长．
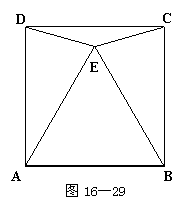
23．如图16—29所示，正方形ABCD内有一点E，且AE=BE=AB，
试求∠EDC和∠ECB的度数．
 |
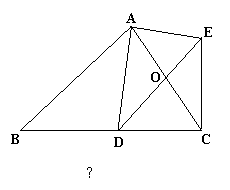
24．如图16—30所示，AD是△ABC中∠BAC的平分线，作DE∥AB，且DE=AC，AD≠CE，试说明：四边形ADCE为等腰梯形．
 |