八（上）第十三章全等三角形章节测试
一、看准了再选(每题3分共30分)
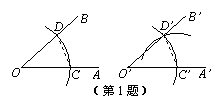
1．用直尺和圆规作一个角等于已知角的示意图如下，则说明∠A′O′B′＝∠AOB的依据是（ ）
A．（S．S．S．） B．（S．A．S．） C．（A．S．A．） D．（A．A．S．
2．如图，
沿直角边
所在的直线向右平移得到
，下列结论中错误的是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
3．如图，D在AB上，E在AC上，且AB=AC，则在下列条件中，无法判定△ABE≌△ACD的是（ ）
A．AD=AE B． ∠B=∠C C．BE=CD D．∠1=∠2
 | |||
 | |||
4． 下列各条件中，不能作出惟一三角形的是（ ）
A．已知两边和夹角 B．已知两角和夹边
C．已知两边和其中一边的对角 D．已知三边
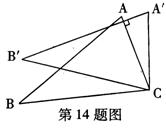
5．如图，将△ABC绕着点C按顺时针方向旋转20°，B点落在
位置，A点落在
位置，若
，则
的度数是（
）
A．50° B．60° C．70° D．80°
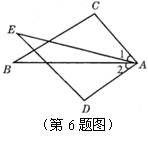
6．如图，已知
，
，增加下列条件：①
；②
；③
；④
．其中能使
的条件有（ ）
Ａ．
个 Ｂ．
个 Ｃ．
个 Ｄ．
个
 |
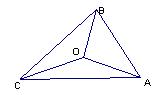
8．如图，△ABC的三边AB、7.BC、7.CA长分别是20、30、40，其
7．三条角平分线将△ABC分为三个三角形，
则S△ABO︰ S△BCO︰S△CAO等于（ ）
A．1︰1︰1 B．1︰2︰3 C．2︰3︰4 D．3︰4︰5
8.．在⊿
中，AB>AC,分别延长中线
至 
，使
，
，连接
。则（ ）
A、
B、AH>AF C、AH<AF D、AH和AF的大小无法比较
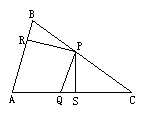
9．如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,
若AQ=PQ,PR=PS,下面三个结论:①AS=AR ②QP∥AR ③△BRP≌△CSP正确的是( )
A.①和③ B.②和③ C.①和② D.①②和③
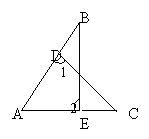
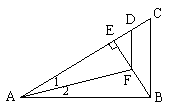
10. 如图,AB⊥BC，BE⊥AC，∠1=∠2，AD=AB，则（ ）
A.∠1=∠EFD B.BE=EC C.BF=DF=CD D.FD∥BC
二、想好了再填(每题4分共32分)
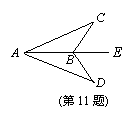
11．如图，点B在AE上，∠CAB=∠DAB，要使△ABC≌△ABD，可补充的一个条件是： ．
 | |||
 | |||
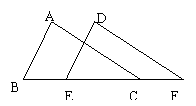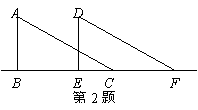
12.如图，∠A=∠D=90°，AB=DE，再加一个能使△ABC≌△DEF的相等条件这个条件是：_____________或__________________使得全等的根据是HL
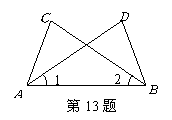
13．如图，在
和
中，现给出如下三个论断：①
；②
；
③
．请选择其中两个论断为条件，另一个论断为结论，构造一个命题．
写出所有的真命题（写成“
”形式，用序号表示）：
___________________________________________________．
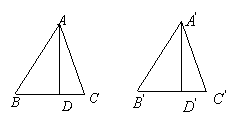
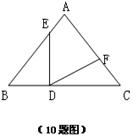
14.已知:如图，△ABC中，∠B=∠C=50°,BD=CF,BE=CD,则∠EDF= 度.
15.如图，△ABC中，∠C = 90°，角平分线AE分对边CE：EA = 1：3，AC=12 cm，E到AB的距离是 ________cm。
16.AD是△ABC的边BC上的中线，AB＝12，AC＝8，则边BC的取值范围是＿＿＿＿；中线AD的取值范围是＿＿＿＿．
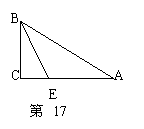
17． 如图，
分别是锐角三角形
和锐角三角形
中
边上的高，且
．若使
，请你补充条件___________．(填写一个你认为适当的条件即可)
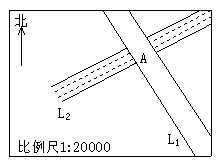
18．如图，某市区一工厂在公路西侧河南岸，到公路L1的距离与河岸L2的距离相等，并且与公路桥较近的桥头A的距离为300米，请在图中标出工厂B的位置（画图时保留尺规作图的痕迹）
三、
想好了再规范的写（共36分）
19. 已知∠BAC=∠DAE，∠ABD=∠ACE，AB=AC . 证明：BD=CE.
20.已知：如图，∠A＝∠D＝90°，BD与AC相交于点O，且BD＝AC。求证：OB＝OC
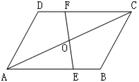21.如图，AB=CD，AD=BC，EF经过AC的中点O，分别交AB、CD于E、F。 求证：OE=OF.
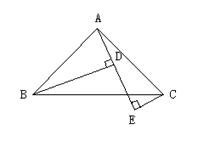
22.. 如图，AB=AC,∠BAC=900,BD⊥AE于D，CE⊥AE于E，且BD＞CE，求证:BD=EC+ED.
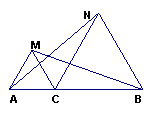
23.⑴已知：如图1，点C为线段AB上一点，△ACM，△CBN是等边三角形，
求证：AN=BM，这时可以证明 __________________，得到AN=BM
⑵如果去掉“点C为线段AB上一点”的条件,而是让△CBN绕点C旋转成图2的情形,还有“AN=BM”的结论吗?如果有,请给予证明.
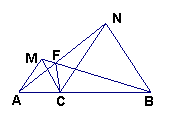
⑶如图3,仍保留原题的所有条件,并设AN、BM交于点F,连接CF,请用刻度尺度量BF、CF、NF的大小,不难发现：BF=CF+NF,为什么?请给予证明.
