四边形的性质探索检测题

八年级上四边形的性质探索检测题

班级　　　　 姓名　　　　　  成绩　　　　　 .

一、填空题。(每题3分,共36分)

1、ABCD中，如果∠B=100°，那么∠A、∠D的值分别是　　　 、　　  .

2、正n边形的内角和等于1080°，那么这个正n边形的边数n=_____.

3、若正方形的对角线为2，则它的面积为 　　　　　 。

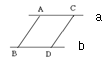
4、如图, AB和CD是夹在两平行线a,b之间的平行线段,则AB　　　CD.(填“”或“”或“=”)

5、菱形的一个内角是60º，边长是5cm，则这个菱形的较短的对角线长是　　　　 cm；

6、等腰梯形的上、下底边长分别为5 cm、11 cm，高为4 cm，则这个等腰梯形的的周长为　　　　。

7、在平行四边形ABCD中，AC、BD是对角线，需要添加　　　　　　　　　　　　 ，就成为矩形。

8、若矩形的面积S =16 cm²,其中一边是a = 2cm,则另一边b =_______cm.

9、四边形ABCD中，已知AB=7cm,BC=5cm,CD=7cm,AD=　　 时，四边形ABCD是平行四边形。

10、矩形的面积为12 cm²，一条边长为3 cm，则矩形的对角线长为_______.

11、已知菱形的两条对角线长为6cm和8cm，则菱形的周长是　　　 ，面积是　　 。

12、已知平行四边形的面积是144,相邻两边上的高分别为8和9,则它的周长是______________.

二、选择题。(每题3分,共36分)

1、 有一正多边形的每个外角都是30⁰, 则这个多边形是(　　　　)

A、 正方形　　　 B、正六边形　　 C、正八边形　　　 D、正十二边形.

2、 若A，B，C是不在同一直线上的三点，则以这三点为顶点画平行四边形，可画（　　　　  ）

A、1个　　　 B、2个　　　 C、3个　　　　D、4个

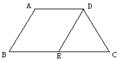
3、如图，等腰梯形ABCD中，AD∥BC，AD=5，AB=6，BC=8，且AB∥DE，△DEC的周长是（　　　　）

A、3　　　　　　B、12

C、15　 　　　D、19

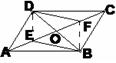
4、如图，□ABCD中，EF过对角线的交点O，AB=4，AD=3，OF=1.3，

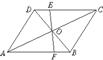则四边形BCEF的周长为(　　　　）

A、8.3 　　 　 B、9.6　　　　C、12.6　　　 　　D、13.6

5、当矩形的对角线互相垂直时, 矩形变成(　　　　 )

A、菱形　　　　 B、等腰梯形　　　　C、正方形　　　 D、无法确定.

6、平行四边形一边长为12cm，那么它的两条对角线的长度可以是（　　　 ）

A、8cm和14cm 　　　 B、10cm 和14cm　　　C、18cm和20cm　　　　 D、10cm和34cm

7、使用同一种规格的下列地砖，不能密铺的是（　　　 ）

A、正六边形地砖　　　　　B、正五边形地砖　　　 C、正方形地砖　　　　　D、正三角形地砖

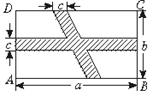8、如图，在矩形ABCD中，横向阴影部分是矩形，另一阴影部分是平行四边形，照图中标注的数据，计算图中空白部分的面积，其面积是（　　）

A、bc－ab+ac+c² B、ab－bc－ac+c²

C、a²+ab+bc－ac　　　 D、b²－bc+a²－ab

9、已知一个四边形ABCD的边长分别为a、b、c、d，其中a、c为对边，且a²+b²+c²+d²=2ac+2bd，则四边形是（　　 ）　

A、 任意四边形　　　B、梯形　　　 C、平行四边形　　　　D、对角线互相垂直的四边形；

10、小明用两根同样长的竹棒做对角线，制作四边形的风筝，则该风筝的形状一定是（ 　　 ）

A、矩形　　　 B、正方形　　　 C、等腰梯形　　　 D、无法确定

11、在线段、角、等边三角形、等腰三角形、平行四边形、矩形、菱形、正方形、等腰梯形、圆这十种图形中,既是轴对称图形又是中心对称图形的共有(　　　　)

A、5种　　　B、6种 　　 C、7种 　　 D、8种

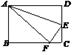12、如图，矩形ABCD沿AE折叠，使D点落在BC边上的F处，如果∠BAF=60°，则∠DAE=（ ）

A、15°　　　B、30°　　C 、45°　　  D、60°

三、解答题。（共30分）

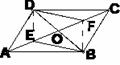
1、如图，在□ABCD中，AC交BD于点O，点E、点F分别是OA、OC的中点，请判断线段BE、DF的关系，并证明你的结论。

2、已知：如图，在梯形ABCD中，AD∥BC，AB＝DC，P是AD的中点。PB与PC相等吗？为什么？

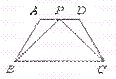
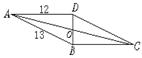
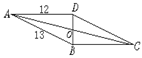
3、如图，四边形ABCD是平行四边形，BD⊥AD，求BC，CD及OB的长．

4、如图，已知□ABCD中，点E、F分别在AD、BC上，且EF垂直平分对角线AC，垂足为O，求证：四边形AECF是菱形。

四、探究与思考。（每题6分，共18分）

1、观察下面图形, 并回答问题.

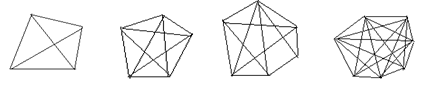①、四边形有　　 条对角线；五边形有　　 条对角线；六边形有　　  条对角线。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

②、根据规律求七边形的对角线的条数是 　　　　　 ；

③、n边形总的对角线的数量是 　　　　　 。

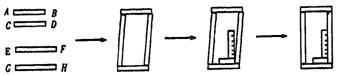
2、工人师傅做铝合金窗框分下面三个步骤进行:

(1)先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;

(2)摆放成如图②的四边形,则这时窗框的形状是 　　　　 形,根据的数学道理是:　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 。

(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是　　　　 形,根据的数学道理是：　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

(图①)　　　　 (图②)　　　　　 (图③)　　　　 图

3、小明家准备在客厅铺设地板砖.客厅地面是一个矩形, 长6.3米, 宽4.8米. 装修工人提出两个建议:一是铺设80cm×80cm的地板砖, 每块40元;二是铺设60cm×60cm的地板砖, 每块25元. 小明要求材料费少, 又铺得整齐为好, 你能帮他出个好主意吗?

八年级上四边形的性质探索检测题

（参考答案）

一、填空题。(每题3分,共36分)

1、100⁰、  80⁰  2、 8　 3、 2　　4、 =　 5、 5cm  6、 26cm 　7、AC=BD、∠ABC=90⁰

8、4　 9、 5cm　10、5cm  11、20cm、 24cm² 12、68

二、选择题。(每题3分,共36分)

1、D　2、C　3、C　4、B　5、C　6、C　7、B　8、B　9、C　10、D　11、B　12、A

三、解答题。

1、解：BE=DF。

证明：连结DE、BF

∵四边形ABCD是平行四边形

∴OB=OD，OA=OC

∵点E、F是OA、OC的中点

∴OE=OA，OF=OC

∴OE=OF

又∵OB=OD

∴四边形DEBF是平行四边形

∴BE=DF

2、解：PB=PC。

理由：在梯形ABCD中，AD∥C，AB=DC

　　 ∴梯形ABCD是等腰梯形

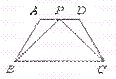　　 ∴∠A=∠D

　　 ∵点P是AD的中点

∴PA=PD

在△ABP和△DCP中

PA=PD，∠A=∠D，AB=DC

∴△ABP≌△DCP（SAS）

∴PB=PC

3、解：∵四边形ABCD是平行四边形

∴BC=AD=12，DC=AB=13

在直角三角形ABD中，

AB²=AD²＋BD²

∴BD²=13²－12²=5²

即BD=5

又∵OB=OD

∴OB=BD=×5=

4、证明：∵EF垂直平分AC

∴∠AOE=∠COF=900，AE=EC，OA=OC

∵四边形ABCD是平行四边形

∴AD∥BC

∴∠AEO=∠CFO

在△AOE和△COF中，

∠AEO=∠CFO，∠AOE=∠COF，OA=OC

∴△AOE≌△COF（AAS）

∴AE=CF

又∵AE∥CF

∴四边形AECF是平行四边形

又∵AE=EC

∴四边形AECF是菱形

四、探究与思考。

1、①2条、5条、9条

②14条

③

2、②平行四边形；两组对边分别相等的四边形是平行四边形。

③矩形；有一个内角是直角的平行四边形是巨型。

3、解；客厅的面积：6.3×4.8=30.24㎡

方案一：30.24÷0.64=47.25≈48块

共耗费：40×48=1920元

方案二：30.24÷0.36=84块

共耗费：25×84=2100元

因为小明要求材料费少, 又铺得整齐为好，所以我觉得选择方案一最恰当。