初二数学潜能知识竞赛试题1
姓名 学号
1.已知
，则下列四个式子中一定正确的是( ).
A.
B.
C.
D.
2．已知
为实数，且
，则
的值为（ ）
A．3 B．– 3 C．1 D．– 1
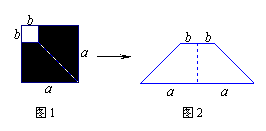
3．如图1，在边长为a的正方形中剪去一个边长为b的小正形（a＞b），把剩下部分拼成一个梯形（如图2），利用这两幅图形面积，可以验证的公式是 （ ）
A．a2＋b2＝(a＋b)(a－b)
B．(a－b)2＝a2－2ab＋b2
C．(a＋b)2＝a2＋2ab＋b2
D．a2－b2＝(a＋b)(a－b)
4．把４x
＋1加上一个单项式，使其成为一个完全平方式．请你写出所有符合条件的单项式 ．
5．一组数据5，8，x，10，4的平均数是2x，则这组数据的方差是
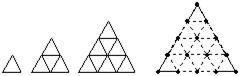6．如图,是用火柴棒摆出的一系列三角形图案,按这种方案摆下去,当每边上摆2006根火柴棒时,共需要摆________根火柴棒.
7．有古诗“葭生池中”今有方池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问：水深、葭长各几何？（1丈=10尺）
回答：水深 ，葭长 。
8．唐寅点秋香的故事家喻户晓了，现在来玩个游戏：
“唐伯虎点秋香”
【规则】下面有四个人，其中一个人是秋香，请你通过下面提示辨别出谁是秋香
友情提示：这四个人分别是：春香、夏香、秋香、冬香
【所给人物】A、B、C、D
①A不是秋香，也不是夏香 ②B不是冬香，也不是春香
③如果A不是冬香，那么C不是春香 ④D既不是夏香，也不是春香
⑤C不是春香，也不是冬香
若上面的命题都是真命题，问谁是秋香？（ ）
（A）A （B）B （C）C （D）D
9.在商品市场经常可以听到小贩的叫嚷声和顾客的讨价还价声：“10元一个的玩具赛车打八折，快来买啊！”“能不能再便宜2元？”如果小贩真的让利(便宜)2元卖了，他还能获利20％，根据下列公式求一个玩具赛车进价是多少元？
（公式：
）
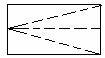
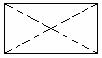
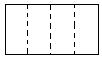10.现有一张长和宽之比为2：1的长方形纸片，将它折两次（第一次折后也可打开铺平再者第二次），使得折痕将纸片分为面积相等且不重叠的四个部分（称为一次操作），如图甲（虚线表示折痕）．除图甲外，请你再给出三种不同的操作，分别将折痕画在图①至图③中（规定：一个操作得到的四个图形，和另一个操作得到的四个图形，如果能够“配对”得到四组全等的图形，那么就认为是相同的操作，如图乙和图甲示相同的操作）．
 | | |
① ② ③
11.如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”．
如：
， 
，
， 因此4，12，20都是“神秘数”
（1）28和2012这两个数是“神秘数”吗？为什么？
（2）设两个连续偶数为2k+2和2k（其中k取非负整数），由这两个连续偶数构造的神秘数是4的倍数吗？为什么？
（3）两个连续奇数的平方数（取正数）是神秘数吗？为什么？
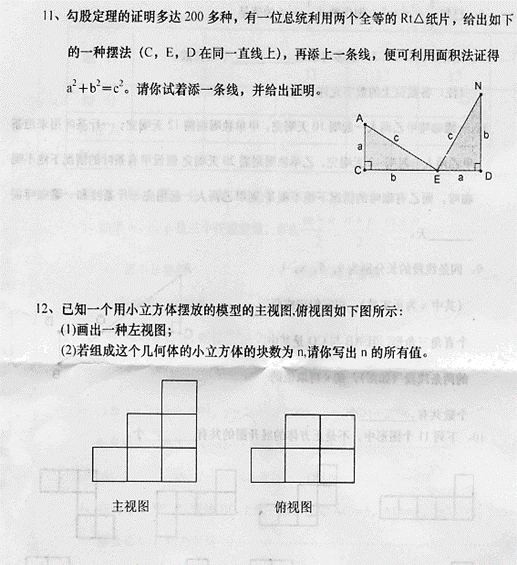
12.我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等，那么在什么情况下，它们会全等？
(1) 阅读与证明：对于这两个三角形均为直角三角形，显然它们全等。
对于这两个三角形均为钝角三角形，可证明它们全等(证明略)
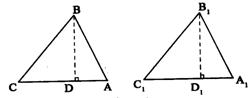
对于这两个三角形均为锐角三角形，它们也全等，可证明如下：
已知：△ABC、△
均为锐角三角形，AB=
，BC=
，∠C=∠
，
证明：△ABC≌△ (请你将下列证明过程补充完整)
证明：分别过点B、
，作BD⊥CA于D，
于
，则∠BDC=
=90º，
∵BC=，∠C=∠
∴△BCD≌△
∴BD=
(2) 归纳与叙述：由(1)可得到一个正确结论，请你写出这个结论。
数学潜能知识竞赛试题2
姓名 学号
1、若
，则
一定是（ ）
A、正数 B、负数 C、非负数 D、非正数
2、某手表每小时比准确时间慢3分钟，若在清晨4点30分时与准确时间对准，则当天上午该手表指示时间是10点50分时，准确时间应该是（ ）
A、11点10分 B、11点9分 C、11点8分 D、11点7分
3、已知一组数据6，8，10，x的中位数与平均数相等，这样的x有( )
A、 1个 B、 2个 C、 3个 D、 4个以上（含4个）
4、若
（是实数），则M的值一定是（ ）
A、正数 B、负数 C、零 D、整数
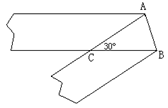5、如图所示,将宽为4厘米的纸条折叠,折痕为AB，如果
∠ACB=30°,折叠后重叠部分的面积为（ ）平方厘米
A、16 B、14 C、12 D、4
6、如图所示，某人从A点出发，每前进10m，就向右转
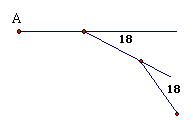18°………这样下去，他第一次回到出发地A时，一共走 了
m
7、,一个人从A点出发沿着北偏东55°方向走到B点,再从B点出发沿着南偏东35°方向走到点C,则∠ABC的度数为( )
A.20° B.90° C.70° D.125°
如图,把一张长方形纸尾ABCD沿着EF折叠,若∠EFG=50°,求∠AEG的度数?
一罐咖啡甲乙两人一起喝10天喝完，甲单独喝则需12天喝完；一斤茶叶用来泡茶甲乙两人一起喝12天喝完，乙单独喝则需20天喝完。假设甲有茶叶的情况下绝不喝咖啡，而乙有咖啡的情况下绝不喝茶。则甲乙两人一起用完一斤茶叶和一罐咖啡需多少天？
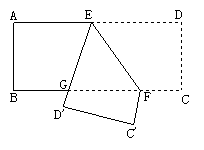
如图，已知在
中, 
, 
于点
, 且
. 若将此三角形沿
剪开成为两个三角形, 在平面上把这两个三角形拼成一个四边形, 你能拼出所有不同形状的四边形吗? 画出所拼四边形的示意图 (标出图中的直角),并分别写出所拼四边形的对角线的长 (不要求写计算过程, 只须写出结果).
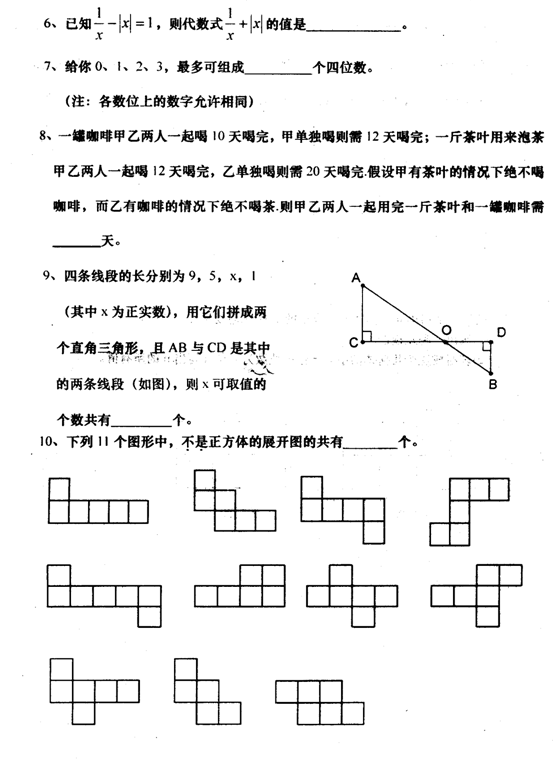
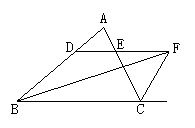
如图所示：∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F，过F作DF∥BC，交AB于D，交AC于E，则：
① 图中有几个等腰三角形？为什么？
② BD，CE，DE之间存在着什么关系？请说明理由．
数学潜能知识竞赛试题3 4 5
28=4×7=
；2012=4×503=所以是神秘数；
（2）
因此由2k+2和2k构造的神秘数是4的倍数．
（3）由（2）知神秘数可表示为4的倍数但一定不是8的倍数因为两个连续奇数为2k+1和2k-1
则
，即两个连续奇数的平方差不是神秘数．
 |  |  |