二次函数测试题 姓名
一、选择题：（每题3分，共30分）
1、对于
的图象下列叙述正确的是
（ ）
A 
的值越大，开口越大
B 的值越小，开口越小
C 的绝对值越小，开口越大
D 的绝对值越小，开口越小
2、对称轴是x=-2的抛物线是（ ）
A..y= -2x2-2 B y= 2x2-2
C. y=2(x-1)2+3 D. y=2(x+1)2-3
3、与抛物线
的形状大小开口方向相同，只有位置不同的抛物线是（ ）
A．
B．
C．
D．
4、二次函数
的图象上有两点(3，－8)和(－5，－8)，则此拋物线的对称轴是（ ）
A．
＝4
B. ＝3 C. ＝－5
D. ＝－1。
5、抛物线
的图象过原点，则
为（ ）
A．0 B．1 C．－1 D．±1
6、把二次函数
配方成顶点式为（ ）
A．
B． 
C．
D．
7、直角坐标平面上将二次函数y＝-2(x－1)2－2的图象向左平移１个单位，再向上平移１个单位，则其顶点为（ ）
A.(0，0) B.(1，－2) C.(0，－1) D.(－2，1)
8、函数
的图象与轴有交点，则
的取值范围是（ ）
A．
B．
C．
D．
9、抛物线
则图象与轴交点为
（ ）
A． 二个交点 B． 一个交点 C． 无交点 D． 不能确定
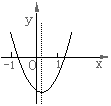10、二次函数
的图象如图所示，则
，
，
，
这四个
式子中，值为正数的有（ ）
A．4个 B．3个 C．2个 D．1个
|
二、填空题：（每题3分，共36分）
1、．已知抛物线
，请回答以下问题：
它的开口向 ，对称轴是直线 ，顶点坐标为 ；
2、．抛物线
过第二、三、四象限，则 0，
0，
0．
3、．抛物线
可由抛物线
向 平移 个单位得到．
4、．顶点为（－2，－5）且过点（1，－14）的抛物线的解析式为 ．
5、．对称轴是
轴且过点A（1，3）、点B（－2，－6）的抛物线的解析式为
．
6、．抛物线
在轴上截得的线段长度是
．
7、．抛物线
，若其顶点在轴上，则
．
8、.已知二次函数
，则当 时，其最大值为0．
9．二次函数
的值永远为负值的条件是 0， 0．
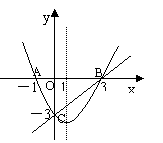10．如图，在同一直角坐标系中，二次函数的图象与两坐标轴分别交于A（－1，0）、点B（3，0）和点C（0，－3），一次函数的图象与抛物线交于B、C两点。
⑴二次函数的解析式为 ．
⑵当自变量 时，两函数的函数值都随增大而增大．
⑶当自变量 时，一次函数值大于二次函数值．
11．已知抛物线与轴交于点A，与轴的正半轴交于B、C两点，且BC=2，
S△ABC=3，则= ，= ．
12、有一个二次函数的图象，三位学生分别说出了它的一些特点：
甲：对称轴是直线x=4；
乙：与x轴两个交点的横坐标都是整数；
丙：与y轴交点的纵坐标也是整数，且以这三个交点为顶点的三角形面积为3．
请你写出满足上述全部特点的一个二次函数解析式：
二、解答题：
1、（6分）已知二次函数y=2x²-4x-6 求：
此函数图象的顶点坐标，与x轴、y轴的交点坐标，
2、（6分）某商人如果将进货价为8元的商品按每件10元出售，每天可销售100件，现采用提高售出价，减少进货量的办法增加利润，已知这种商品每涨价1元其销售量就要减少10件，问他将售出价定为多少元时，才能使每天所赚的利润最大？并求出最大利润．
3、（6分）心理学家发现，学生对概念的接受能力y与提出概念所用的时间x(单位：分)之间满足函数关系：y=-0.1x2+2.6x+43(0＜x＜30）。y值越大，表示接受能力越强。
(1)x在什么范围内，学生的接受能力逐步增强？x在什么范围内，学生的接受能力逐步降低？
(2)第10分时，学生的接受能力是什么？
(3)第几分时，学生的接受能力最强？
4、（7分）已知抛物线
与y轴交于C（0，c）点，与x轴交于B（c，0），其中c＞0，
（1） 求证： b＋1＋ac=0；
（2）
若C与B两点距离等于
，一元二次方程
的两根之差的绝对值等于1，求抛物线的解析式.
5、（9分）已知：抛物线
与x轴的一个交点为A（-1，0）
（1）求抛物线与x轴的另一个交点B的坐标；
（2）D是抛物线与y轴的交点，C是抛物线上的一点，且以AB为一底的梯形ABCD的面积为9，求此抛物线的解析式；
（3）E是第二象限内到x轴，y轴的距离
的比为5：2的 点，如果点E在（2）中的抛物线上，且它与点A在此抛物线对称轴的同侧，问 ：在抛物线的对称轴上是否存在点P， 使
的周长最小？若存在，求出点P的坐标，若不存在，请说明理由。