第一学期八年级数学教学案
3.5 矩形、菱形、正方形（3）
教学目标：
1、 经历探索菱形的特征的过程,在操作活动和观察、分析过程中发展
学生的主动探究习惯和初步审美意识，进一步了解和体会说理的基本方法。
2、理解菱形的意义，利用特征解决有关问题。
教学重点：探索菱形的性质及其性质的简单应用。
教学难点：菱形与平行四边形之间的内在联系与区别。
教学过程：
一、情境创设：
图片中是你熟悉的图形吗？通过观察：你能得出这些图形的特征吗？
二、新课讲解：
1、菱形的概念:
画一个△ABC,取BC的中点M,把△ABC绕点M旋转180°后得一个△A′B′C′, △A′B′C′与△ABC拼成一个怎样的图形?当△ABC中AB=AC时, △A′B′C′与△ABC又拼成一个怎样的图形?
结论：（1） 叫做菱形；
（2）菱形既是 图形，对称轴是 ，又是 图形，对称中心是 。
2、菱形的特征：
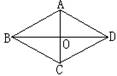注意：菱形是平行四边形，它具有平行四边形的一切性质；菱形又是特殊的平行四边形，它还具有哪些特殊性质？
讨论：如图，菱形ABCD的对角线相交于点O。
⑴图中的哪些线段相等？哪些角相等？
⑵菱形的两条对角线有什么特殊位置关系？你能说明理由吗？
（3）若AC=6,BD=8,则AB= ,S菱形ABCD= 。
结论： （1）、菱形的 相等。菱形的对角线 ，并且 。
（2）、菱形的面积＝ ＝ 。
三、例题讲解：
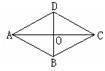
例1、已知：如图，菱形ABCD的周长为8cm，∠ABC：∠BAD=2：1，对角线AC、BD相交于点O，求BD、AC的长及菱形的面积。
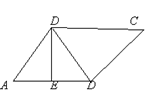
例2、如图，在菱形ABCD中，E是AB的中点，且DE⊥AB.
（1）求∠ABD的度数；
（2）若菱形的边长为2，求菱形的面积.
四、课堂练习
1、菱形具有而平行四边形不一定具有的性质是＿＿＿＿（填代号）
①对边平行且相等；②4条边都相等；③对角线互相垂直；④对角相等
⑤对角线相等；⑥对角线互相垂直；⑦轴对称图形；⑧中心对称图形；
2、如果菱形的两条对角线的长分别是6cm和8cm，那么这个菱形的面积等于 cm2，周长等于 cm。
3、若菱形ABCD的周长为40cm，AC=10cm，则∠ABD= °，∠ABC= °。
4、菱形的面积为24，一条对角线长为6，求菱形的边长和它的另一条对角线长。
五、课堂小结：
1、菱形的概念及性质；
2、数学思想与方法
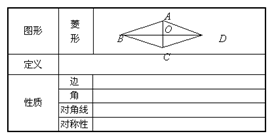
菱形 转化成
3、菱形与平行四边形的关系
六、布置作业：P100 6、9
思考题：在宽为6厘米的矩形纸带上，用菱形设计如下图所示的图案，如果菱形的边长为5厘米，请你回答下列问题：
（1）如果用5个这样的菱形设计图案，那么至少需要多长的纸带？
（2）设菱形的个数为x,所需的纸带长为y，请你用x的代数式表示y，现有长为25厘米的纸带，要设计这样的图案，最多需要多少个菱形？
主备人：俞永亮 审核人：夏存才