八年级数学第一学期教学案
3.5 矩形、菱形、正方形（5）
学习目标： 1、掌握正方形的性质和判定方法；2、能利用正方形的性质和判定解决问题；3、进一步加强分析问题和解决问题的能力。
学习重点：正方形的性质和四边形是正方形的判定方法.
学习难点：培养学生有条理地表达能力
学习过程：
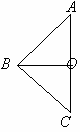一、情境创设：
1、你能用矩形纸片折出1个正方形吗？用虚线画出折叠线。2、你能把一个菱形木框变成正方形木框？动手试一试，并画出用虚线画出变化的过程图形和用文字说明变动的方法。
二、新课讲解：
1、正方形的概念：
如上图，BO是等腰直角三角形ABC的底边AC上的中线.
（1）画出△ABC关于点O对称图形；（2）把点B关于点O的对称点记为D，连结DA、DC，想一想四边形ABCD是中心对称图形吗？说说理由。（3）四边形ABCD有什么特点？
定义： 的平行四边形是正方形
2、正方形的识别：
结论：（1）有一组邻边 的矩形是正方形。（2）有一个角是 的菱形是正方形。
（3）有一组邻边 且有一个角是 的平行四边形叫做正方形
3、正方形的性质：
正方形既是特殊的矩形，又是特殊的菱形，因而正方形具有矩形、菱形的一切性质，你能写出正方形的所有性质吗？
结论：正方形的对边 ；正方形的四条边 ；四个角都是 ；
对角线 。
三、例题讲解：
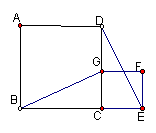
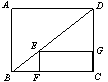
例1、如图，四边形ABCD和四边形CEFG都是正方形，试探索BG与DE的关系
 |
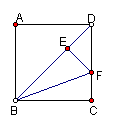
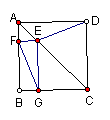例2、如图，四边形ABCD是正方形，点E是AC上的点EG⊥BC，EF⊥AB，（1）试猜测DE与FG关系如何？并说明理由。（2）如果正方形ABCD的边长为4㎝，求四边形BGEF的周长
。
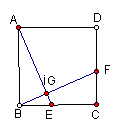
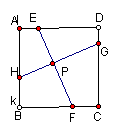
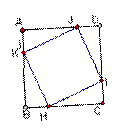例3、如图，正方形ABCD中，AK=BH=CI=DJ，那么四边形KHIJ是什么样的四边形？为什么？
四、课堂练习：
1、（1）正方形的边长为2，则对角线长为 。
（2）正方形的边长与对角线长之比为 。
（3）正方形的对角线长为a，则正方形的面积为 。
2、如图：正方形ABCD的周长为15cm , 则矩形EFCG的周长是______
3、E为正方形ABCD的边BC延长线上一点，且CE=AC，AE交CD于F，则∠AFC= .
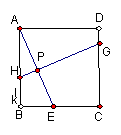
4、如图，正方形ABCD中，E是对角线BD上的一点，且BE=BC，EF⊥BD，DE与CF相等吗？为什么？
 |  |  | |||
五、课堂小结：
六、布置作业：P101 10、11、12
思考题：（1）如图（1）正方形ABCD中，AE⊥BF于点G，试说明AE=BF。
（2）如果把线段BF变动位置如图（2），其余条件不变，（1）中结论还成立吗？
（3）如果把AE与BF变动位置如图（3），（1）中的结论还成立吗？
主备人：俞永亮 审核人：夏存才