初二数学第一学期期中考试试卷
满分：100分 时间：100分钟 命题人： 汤炳祥 李军
一、选择题（每题3分共10题，合计30分）（请将答案填入下表）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1.
下列四个图像中，不表示某一函数的图像的是 （
）
2.
一次函数
不经过第一象限，则b的取值范围是( )
A． b>0 B．b<0 C．b≥0 D．b≤0
3.
把函数
的图像向上平移2所得图像的解析式是( )
A． 
B．
C．
D．
4.
直线
中，k取不同的值得到不同的直线，这些直线必定 （
）
A．相交于同一点 B．可能多于一个交点 C．互相平行 D．没有确定的位置关系
5. 某班共有60名同学，在统计同学们喜爱的学科时，得到如下数据：语文50人，数学55人，英语53人，物理48人，用统计图表示这组数据宜用 （ ）
A．扇形统计图 B． 条形统计图 C． 折线统计图 D． 三种统计图均可以
6. 相信同学们一定会使用直尺和圆规作一个角的平分线，请问其依据是 ( )
A．SAS B．ASA C．AAS D．SSS
7. 在△ABC和△DEF中，（１）AB=DE（２）BC=EF（３）AC=DF（４）∠A=∠D（５）∠B=∠E（６）∠C=∠F，则下列条件中不能判断△ABC≌△DEF的是 ( )
A．(1) (2) (3) B．(1) (2) (5) C．(2) (4) (5) D．(1) (3) (5)
8. 下列命题中，假命题的个数有( )
（１）面积相等的两个三角形全等．
（２）全等三角形的对应边相等，对应角相等．
（３）三角形任意一边的两个端点到这边上的中线的距离相等．
（４）有两边和其中一边上的高分别对应相等的两个三角形全等．
（５）三角形的三条角平分线相交于一点，这点到三角形三边的距离一定相等．
A．１ B．２ C．３ D．４
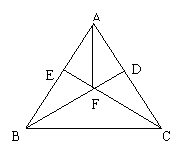
9. 如图，BD、CE是△ABC的高，它们相交于F，且BD＝CE
则图中全等的三角形有( )对．
A．２ B．３ C．４ D．５
10.
如图，在△ABC中∠C=90°，AC=BC，AD平分∠CAB，
DE⊥AB于E，若AB=6㎝，则△DBE的周长( )
A．小于6 cm B．等于6 cm
C．大于6 cm D．缺少条件，无法确定
二、填空题（每题2分共8题，合计16分）
11. 在扇形统计图中，若各个扇形的面积之比为4：3：2：1，则最小的扇形的圆心角是 ．
12.
函数
中自变量x的取值范围是
．
13. 写出一个经过点（-1，3）且不经过第一象限的一次函数解析式： ．
14.
直线
与两坐标轴围成的三角形的面积为6，则a =
．
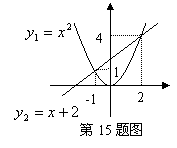
15. 函数
与
的图像及交点如图所示，则不等式
的解集
是______________．
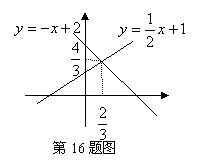
16.
根据图像，请你直接写出二元一次方程组
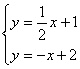的解为：
．
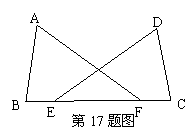
17. 如图，已知B、E、F、C在同一直线上，BE=CF，AF=DE，则添加条件 ，可以判断△ABF≌△DCE
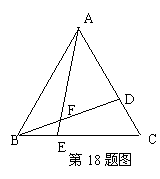
18. 已知△ABC是等边三角形，点D、E分别在AC、BC上，且CD=BE，则∠AFD= ．
三、解答下列各题（共8题，共54分）
19. （6分）已知直线l平行于直线y=－3x，且它与直线y=2x的交点是（a，3），求直线l的解析式．
20. （6分）一家电信公司给顾客提供两种上网收费方式：方式A以每分0.1元的价格按上元网时间计费；方式B除收月租费20元外再以每分0.05元的价格按上网时间计费.设上网时间为x分钟，方式A收费为y1元，方式A的收费为y2元.
（1）分别写出y1 和y2关于x的函数解析式；
（2）如何选择收费方式能使上网者更合算?
21. （8分）已知直线y=kx＋6与直线y=2x相交于点P(m，4)，与x轴相交于点A．
(1) 求点P和点A的坐标；
(2) 若点B（x，y）是线段PA上一个动点（A点除外），设△OAB的面积为S．求S关于x的函数关系式以及自变量x的取值范围．
22. （6分）某报社为了了解读者对一种报纸四个版面的喜欢情况，对读者作了一次问卷调查，要求读者选择自己最喜欢的一个版面，下图是甲乙两位同学所作统计图的部分，请你根据甲、乙提供的信息，帮助他们完成两个统计图。【要求：（1）在条形图标出最喜欢第三版的人数（2）在扇形图中标出相应圆心角的度数】
 |
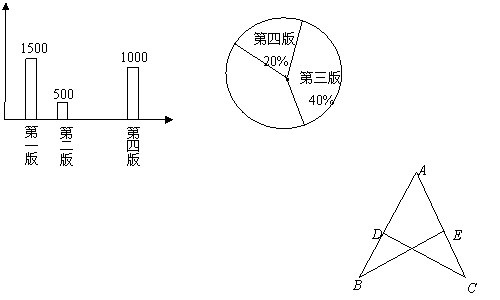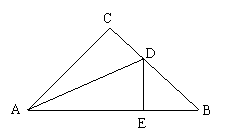
23. （6分）如图，点D在AB上，点E在AC上，AB=AC，∠B=∠C．
求证：BD=CE
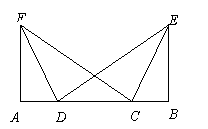
24. （6分）如图，已知A、B、C、D在同一直线上，AD=BC，FA⊥AB，EB⊥AB，垂足分别为A、B，FC=ED，
求证:FD=EC
 |
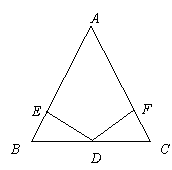
25. （8分）如图DE⊥AB，DF⊥AC，垂足分别为E、F，请你从(1) AB=AC (2) BD=CD (3) DE=DF中选出两个作为已知条件，另一个作为结论，编写一个几何证明题并完成证明过程．
已知:DE⊥AB，DF⊥AC，垂足分别为E、F，且 ，
求证:
证明:
26.
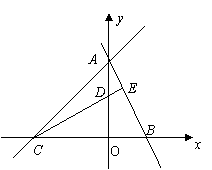（8分）如图，已知直线AB的解析式是
，直线AC的解析式是
，过C点作CE⊥AB，垂足为E，交y轴于点D．求点D的坐标．