初二数学前四章水平测试卷
一、填空题
1.在同一平面内，a、b、c是直线,且a∥b,b⊥c,则a与c的位置关系是________.
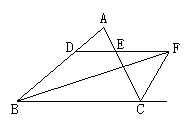
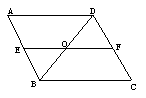
2.如图,AD∥BC,EF∥BC,BD平分∠ABC,图中与∠ADO相等的角有_______ 个,分别是___________.
3．在Rt△ABC中，∠C=Rt∠，∠A=3∠B+10°，则∠B=_______．
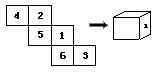
4．如图为一个正方体的表面展开图，现将它折叠成立方体，则左侧面上标有的
数字是 ．
5．直六棱柱的其中一条侧棱长为5cm，那么它的所有侧棱长度之和为 cm．
6．一组数据：
，
，0，
，1的平均数是0，则= ，方差
.
7.已知
的平均数
10，方差3，则
的平均数为
，方差为
.
8．现用火柴棒摆一个直角三角形，两直角边分别用了7根、24根长度相同的火柴棒，则斜边需要用______根．
9．如图在 △ABC中，∠ACB=90°，CE⊥AB，垂足是E，D是AB的中点，如果AB=10，
∠B =30°DE=_______．
10. E. F分别是Rt△ABC的斜边AB上的两点，AF=AC，BE=BC, 则∠ECF=______．
二、选择题
11．下列说法错误的是( )
Ａ.内错角相等，两直线平行． Ｂ. 两直线平行，同旁内角互补．
C. 相等的角是对顶角． D. 等角的补角相等．
12．下列图形中，不是轴对称图形的是（ ）
（A）线段 （B）角 （C）等腰三角形 （D）直角三角形
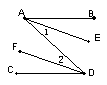13.已知:如图,∠1=∠2,则有( )
A.AB∥CD B.AE∥DF C. AB∥CD 且AE∥DF D.以上都不对
14．下列几何体中，不属于多面体的是（ ）
A．正方体 B．三棱柱 C．长方体 D．圆柱
15、样本方差的作用是（ ）
A、估计总体的平均水平 B、表示样本的平均水平
C、表示总体的波动大小 D、表示样本的波动大小，从而估计总体的波动大小
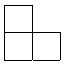
16．由四个大小相同的小正方体搭成的几何体的左
视图如图所示，则这个几何体的搭法不能是（ ）
 | |||
| |||
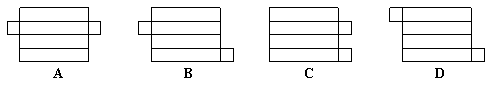
17．下列各图中，不是直四棱柱的表面展开图的是（ ）
18.已知∠A=37°，∠B=53°，则△ABC为（ ）
（A）锐角三角形 （B）钝角三角形 （C）直角三角形 （D）以上都有可能
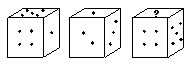19．如图一枚骰子抛掷三次，得三种不同的结果，
则写有“?”一面上的点数是（ ）
|
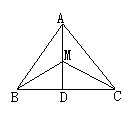
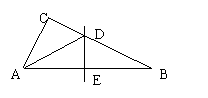
20．如图所示，已知△ABC中，AB=6，AC=9，AD⊥BC于D，M为AD上任一点，则MC2-MB2等于（ ）
（A）9 （B）35 （C）45 （D）无法计算
三、解答题
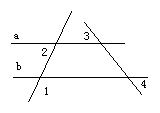
21．如图，a∥b，∠1=122°，∠3=50°，求∠2和∠4的度数。
|
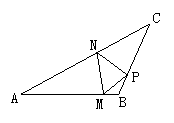
22．如图所示，△ABC中，∠ABC=100°，AM=AN，CN=CP，求∠MNP的度数．
23．
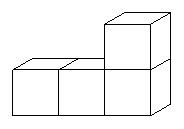画出如图所示的几何体的三视图．
24．已知一个几何体的三视图和有关的尺寸如图所示，求出这个几何体的表面积．按1:2的比例画出这个几何体的表面展开图．
 |
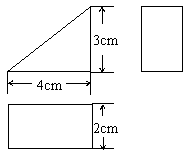25、某校要从甲、乙两名跳高运动员中挑选一人参加一项校际比赛，在最近的8次选拔赛中，他们的成绩（单位：m）如下：
甲：1.70，1.65，1.68，1.69，1.72，1.73，1.68，1.67
乙： 1.60，1.73，1.72，1.61，1.62，1.71，1.70，1.75
（1）他们的平均成绩分别是多少？
（2）哪个人的成绩更为稳定？
（3）经预测，跳高1.65m就很可能获得冠军，该校为了获取跳高比赛冠军，可能选哪位运动员参赛？若预测跳高1.70m方可获得冠军呢？
26．如图所示：∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F，过F作DF∥BC，交AB于D，交AC于E，则：
①图中有几个等腰三角形？为什么？②BD，CE，DE之间存在着什么关系？请证明．
