初二年级上期半期考试数学试题 (试题卷)
命题人：包涌 审题人：周勇
（考试时间：120分钟；总分：150分）
一、填空题（每小题3分，共30分）
1．已知（3，
）是函数
的图像上一点，则k＝___________
2．已知函数
是一次函数，则m的值为_________．
3．将直线
向上平移4个单位得到新直线的解析式为
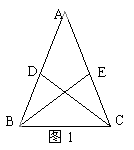
4．如图1，已知D、E是△ABC中边上的两点，AB＝AC，请你再加一个条件_____ __ __，使△ABE≌△ACD．
5．在△ABC和△ADC中，下列三个论断：（1）AB＝AD；（2）∠BAC＝∠DAC；（3）BC＝DC，将其中两个论断作为条件，另一个论断作为结论，构成一个命题，写出一个真命题
6．某市初中毕业升学考试各学科及满分值情况如下表：
| 科 目 | 语文 | 数学 | 英语 | 政史 | 自然学科 |
| 满分值 | 150 | 150 | 150 | 100 | 200 |
若把该市初中毕业升学考试各学科满分值按比例绘成扇形统计图，则数学科所在的扇形的圆心角度数是
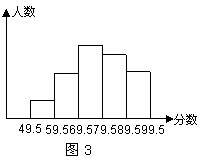7．如图2，AD＝AE，BD＝CE，∠1＝∠2＝110°，∠B＝40°，那么∠CAE＝___________
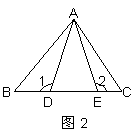
8．如图3,某校对初三学生进行了一次数学应用问题小测验，如图3，将某班60名学生成绩进行整理后，分成5组画出的频数分布直方图，已知从左至右4个小组的频率分别是0.05，0.15，0.35，0.30，那么在这次测验中成绩优秀（分数大于或等于80分的为优秀，且分数为整数）的有_____人．
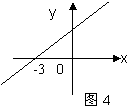
9．函数
的图像如图4所示，则关于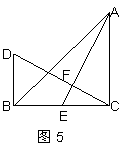
x的不等式
的解集是_______________
10．如图5，△ABC中，∠ACB＝90°，AC＝BC，AE是BC边的中线（即E点为BC的中点），过C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于D，AC＝42cm，则BD的长度为_______cm．
二、选择题（每小题4分，共40分）
11．已知函数y＝
，当x＝a时的函数值为1，则a的值为（ ）
A．3 B．－1 C．－3 D．1
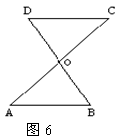
12．已知：如图6，AC、BD交于O点，OA＝OC，OB＝OD，则不正确的结果是（ ）
A、AB＝CD B、AB∥CD C、∠A＝∠D D、∠A＝∠C
13．函数y = k（x – k）（k＜0)的图象不经过（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
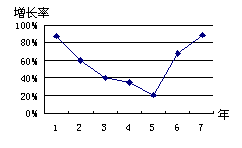14．右图是某厂连续7年产量增长率（相对于上年的增长率）统计图，仔细观察图形，下列说法正确的是（
）
A、这几年产量有增有减
B、产量不断增加
C、开始产量下降，后来产量回升
D、以上说法都不对
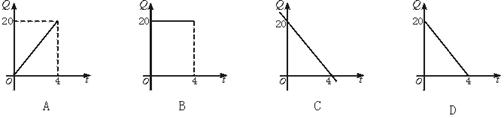
15．一水池蓄水20 m3，打开阀门后每小时流出5 m3，放水后池内剩下的水的立方数Q (m3)与放水时间t(时)的函数关系用图表示为( )
16．到△ABC的三条边距离相等的点是△ABC的( )
A．三条中线交点 B．三条角平分线交点
C．三条高的交点 D．三条边的垂直平分线交点
17．如图7，已知在△ABC中，∠BAC和∠ACB的平分线相交于D点，∠ADC＝130°，那么∠ABC的大小是（ ）
A、80° B、50° C、40° D、20°
18．已知一次函数y＝kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图像是( )
(A) (B) （C） （D）
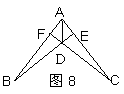19．如图8，AB＝AC，BE⊥AC于E，CF⊥AB于F，BE、CF相交于D，则（1）
（2）
（3）点D在∠BAC的平分线上，以上结论正确的是（ ）
A．只有（1） B．只有（2）
C．只有（1）和（2） D．（1）（2）（3）
20．星期天晚饭后，小红从家里出发去散步，图描述了她散步过程中离家s（米）与散步所用的时间t(分)之间的函数关系．依据图9，下面描述符合小红散步情景的是（ ）
(A) 从家出发,到了一个公共阅报栏,看了一会报后,继续向前走了一会,然后回家了.
(B)从家出发,到了一个公共阅报栏,看了一会报后,就回家了.
(C)从家出发,散了一会步,就找同学去了,18分钟后
(D)从家出发,一直散步(没有停留),然后回家了.
三、解答下列各题(每题10分，共80分)
21．（10分）已知一次函数的图像经过A（
，4），B（1，－5）两点，（1）求这个一次函数的解析式
（2）试判断点P（
，1）是否在这个一次函数的图像上？
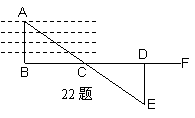22．（10分）如图，要测量河两岸相对的两点A、B的距离，可以在AB的垂线BF上取两点C、D，使CD＝BC，再定出BF的垂线DE，使A、C、E在一条直线上，这时测得的DE的长就是AB的长，请说明理由。
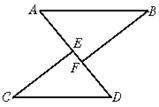
23．（10分）已知：如图，点A、E、F、D在同一条直线上，AE＝DF，BF⊥AD，CE⊥AD垂足为F、E，BF＝CE，求证：AB＝DC．
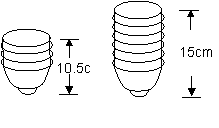
24．（10分）两摞相同规格的饭碗，整齐地叠放在桌面上，请根据图中给出的数据信息，解答问题，（1）求整齐叠放在桌面上饭碗的高度y（cm）与饭碗数x（个）之间的一次函数关系式（不要求写出自变量x的取值范围）
（2）若桌面上有12个饭碗，整齐叠放成一摞，求出它的高度。
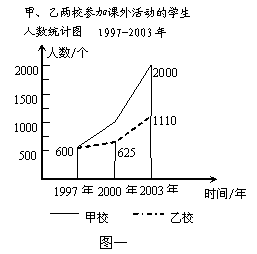
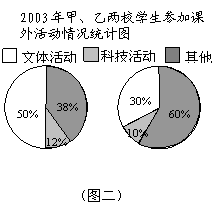
25．下面两幅统计图（如图一、图二），反映了某市甲、乙两所中学学生参加课外活动的情况.请你通过图中信息回答下面的问题（实线是甲学校，虚线是乙学校）.
（1）通过对图一的分析，写出一条你认为正确的结论；（3分）
（2）通过对图二的分析，写出一条你认为正确的结论（左边扇形图甲学校，右边扇形图是乙学校）；（3分）
（3）2003年甲、乙两所中学参加科技活动的学生人数共有多少？（4分）
|
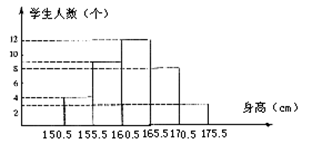
26．(10分)某校初三（1）班36位同学的身高的频数分布直方图如图所示。
问：（1）身高在哪一组的同学最多？
(2)身高在160cm以上的同学有多少人？
(3)求该班同学的平均身高约为多少（精确到0.1cm）？
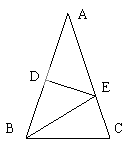
27．（10分）如图，在△ABC中，AB＝AC，D是AB的中点，且DE⊥AB，已知，△BCE的周长为8cm，且AC－BC＝2cm，求AB、BC的长。
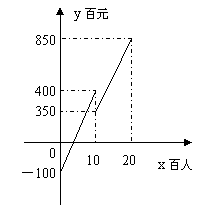28．（10分）某品牌服装厂为推销自已的秋季新款服装，特委托一策划公司筹备一次时装表演会，策划公司预算每张门票定价100元，而且观众总人数要求控制在2000人以内，策划公司毛利润y（百元）与观众人数x（百人）之间的函数关系如图所示。为保证安全，根据相关规定，当观众人数超过1000人时，策划公司需向保险公司缴纳平安保险5000元（不列入成本费），请解答下列问题：（1）求当观众人数不超过1000人时，毛利润y（百元）与观众人数x（百人）之间的函数关系式和成本费用S（百元）关于观众人数的解析式；（2）若策划公司想在这次时装表演中获得38000元的毛利润，则需要售出多少张门票？需支付成本费用多少元？（注：当观众人数不超过1000人时，表演会毛利润＝门票收入－成本费用；当观众人数超过1000人时，表演会毛利润＝门票收入－成本费用－平安保险费）