八年级数学秋期半期考试卷
班级_________姓名_________学号_________成绩_________
（亲爱的同学，这份试卷将再次记录你的自信、沉着、智慧和收获. 请认真审题，看清要求，仔细答题，要相信我能行。）
一.你能填得又对又快吗?（每空3分，共57分）
1.函数y=
中，自变量x的取值范围是_________.
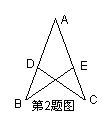
2.如图，AB＝AC，若使△ABE≌△ACD，则还需要添加的条件是________________(只写出一组即可)．
3.如图，若△ABC≌△ADE，∠EAD＝32°，AD＝5cm，则AB＝________，________＝∠EAD＝32°．
4.分析数据时，为了能清楚地表示出各部分在总体中所占的百分比，通常选用_______图；
5.正比例函数y=2x的图象依次经过第________象限．
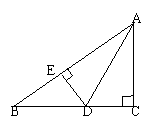
6.如图,在△ABC中，∠C＝90°，AD是∠BAC的角平分线，若BC＝5㎝，BD＝3㎝，则点D到AB的距离DE长为 .
7.函数y=2x+6与x轴的交点坐标是________．
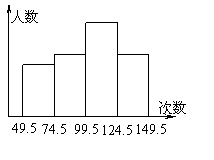8.为了了解中学生的体能情况，抽取了某中学八年级学生进行跳绳测试，将所得数据整理后，画出如图所示的频率分布直方图，已知图中从左到右前三个小组的频率分别是0.1，0.3，0.4，第一小组的频数为5。
(1)第四小组的频率是__________
(2)参加这次测试的学生是_________人
(3)成绩落在______组数据范围内的人数最多
(4)成绩在100次以上(包括100次)的学生占测试
人数的百分率为__________.
| 数量x（个） | 1 | 2 | 3 | 4 | 5 |
| 售价y（元） | 8+0.2 | 16+0.4 | 24+0.6 | 32+0.8 | 40+1.0 |
9.某商店出售货物时，要在进价的基础上增加一定的利润，下表体现了其数量x（个）与售价y（元）的对应关系，根据表中提供的信息可知y与x之间的关系式是__________．
10.函数y=kx+b（k≠0）的图象平行于直线y=2x+3，且交y轴于点（0，-1），则其解析式是_______________．
11.如图把Rt△ABC（∠C=90°）折叠，使A、B两点重合，得到折痕ED,再沿BE折叠，C点恰好与D点重合，则∠A等于______度．
12、在“线段、锐角、三角形、等边三角形、圆”这五个图形中，是轴对称图形的有 个，其中对称轴最多的是
.线段的对称轴是
13、如图，从镜子中看到一钟表的时针和分针，此时的实际时刻是________。
二.相信你一定能选对!（每小题3分，共33分）
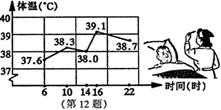
14.右图是护士统计一位病人的体温变化图，这位病人中午12时的体温约为 （ ）
A．39.0℃ B．38.5℃ C．38.2℃ D．37.8℃
15.已知函数y=
，当x=-2时，函数值为（ ）
A．
B．± C．3 D．±3
16.下列点一定在函数y=
的图象上的是（ ）
A．（-2，2） B．（1，-1） C．（-1，-1） D．（0，0）
17.甲、乙两地相距S千米，某人行完全程所用的时间t（时）与他的速度v（千米/时）满足vt=S，在这个变化过程中，下列判断中错误的是 （ ）
A．S是常量 B．t是变量 C．v是变量 D．S是变量
18.如图，△ABC和△DEF是两个全等的三角形，顶点A与F，B与D，C与E能互相重合，则下面书写正确的是( )
A.△ABC≌△DEF B．△ABC≌△FDE
C.△ABC≌△DFE D．△ABC≌△FED
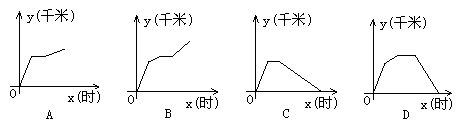
19.一天，张老师从学校坐车去开会，由于途中塞车，他只好步行赶到会场，开完会后，他直接回到学校，下图中能体现他离学校的距离y（千米）与时间x（时）的关系的图象是（ ）
20.我校八(8)班男女生人数之比是3∶2，则制作扇形统计图时女生对应的扇形的圆心角是（ ）
A．144° B．216° C．72° D．108°
21.下列说法：①用一张像底冲洗出来的2张1寸相片是全等形；②所有的正五边形是全等形；③全等形的周长相等；④面积相等的图形一定是全等形．其中正确的是（ ）
A．①②③
B．①③④ C．①③ D．③
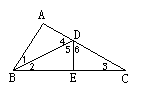
22.如图，D、E是△ABC中AC、AB上的点，△ADB≌△EDB，
△BDE≌△CDE，则下列结论：①AD=DE；②BC=2AB；③∠1=∠2=∠3；④∠4=∠5=∠6．其中正确的有（ ）
A．4个 B．3个 C．2个 D．1个
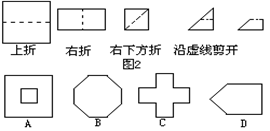23、如图３把一个正方形三次对折后沿虚线
剪下，则所得图形大致是（ ）
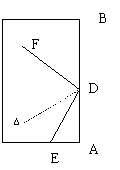
24、小朋友文文把一张长方形的对折了两次，如图所示：使A、B
都落在DA/上，折痕分别是DE、DF，则∠EDF的度数为（ ）
A.60° B. 75° C. 90° D.120°
三. 认真解答，一定要细心哟！（共60分）
25(5分)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF,求证:∠A=∠D.
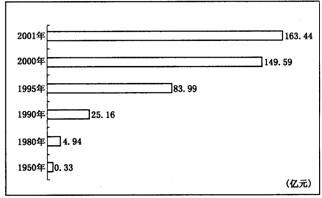
26.(6分)如图，是2001年我省福州市年鉴记载的本市社会消费品零售总额（亿元）统计图．请你仔细观察图中的数据，并回答下面问题．
（1）图中所列的六年消费品零售总额的最大值与最小值的差是多少亿元？
（2）求1990年、1995年和2000年这三年社会消费品零售总额的平均数．（精确到0．01）
（3）从图中你还能发现哪些信息，请说出其中两个．
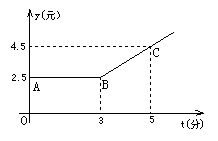
27.(9分)如图，折线ABC是甲地向乙地打长途电话所需要付的电话费y（元）与通话时间t（分钟）之间关系的图象（注意：通话时间不足1分钟按1分钟计费）．
（1）通话1分钟，要付电话费多少元？通话5分钟要付多少电话费？
（2）通话多少分钟内，所支付的电话费一样多？
（3）通话3.2分钟应付电话费多少元?
28.(12分)(1)某礼堂共有25排座位，第一排有20个座位，后面每一排都比前一排多1个座位，写出每排的座位数m与这排的排数n的函数关系式并写出自变量n的取值范围．
(2)上题中，在其他条件不变的情况下，请探究下列问题：
①当后面每一排都比前一排多2个座位时，则每排的座位数m与这排的排数n的函数关系式是______________（1≤n≤25，且n是正整数）
②当后面每一排都比前一排多3个座位、4个座位时，则每排的座位数m与这排的排数n的函数关系式分别是___________，___________（1≤n≤25，且n是正整数）
③某礼堂共有P排座位，第一排有a个座位，后面每一排都比前一排多b个座位，试写出每排的座位数m与这排的排数n的函数关系式，并写出自变量n的取值范围．
29.(8分)已知一次函数的图象经过点A（-3，2）、B（1，6）．则:
①求此函数的解析式，并画出此函数图象. ②求函数图象与坐标轴所围成的三角形面积．
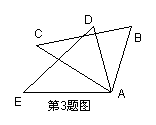
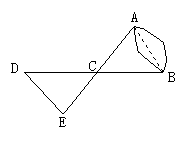
30.(10分)如图，A、B两点分别位于一个池塘的两侧，池塘西边有一座假山D，在DB的中点C处有一个雕塑，张倩从点A出发，沿直线AC一直向前经过点C走到点E，并使CE=CA，然后她测量点E到假山D的距离，则DE的长度就是A、B两点之间的距离．
（1）你能说明张倩这样做的根据吗？(3分)
（2）如果张倩恰好未带测量工具，但是知道A和假山、雕塑分别相距200米、120米，你能帮助她确定AB的长度范围吗？(3分)
（3）在第（2）问的启发下，请你解决下列问题：在△ABC中，AD是BC边的中线，AD=3cm，AB=5cm，求AC的取值范围．(4分)
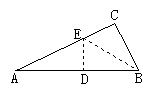
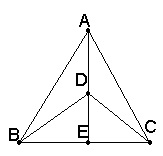32. (10分) 已知△ABC中， AE为角平分线，D为AE上一点，
且∠BDE=∠CDE，
（1）求证：AB=AC
（2）若把 “AE角平分线”换为“AE为高线”，其它条件不变，结论还会成立吗？如果成立，请证明；若不成，请说明理由.