八年级数学（上）评价性试题（一）
§11.1－§11.2
班级 姓名 号次
一、 耐心填一填
1．直角三角形两锐角的度数分别为x、y，其关系式为y=90－x，其中变量为 ，常量为 。
2．函数
的自变量x的取值范围是
。
3．表示函数常用的方法有 。
４．若点A（m，2）在函数y=2x－6的图象上，则m的值为 。
5．用描点法画函数图象的一般步骤是
。
6．已知函数
当x=2时，函数值为
。
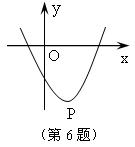
7．如图，某函数图象上的最低点P的坐标是（1，－3），
则当x＞1，y随x的增大而 （填增大或减少）
8．某水果批发市场香蕉的价格如下表：
| 购买香蕉数 (千克) | 不超过 20千克 | 20千克以上 但不超过40千克 | 40千克以上 |
| 每千克价格 | 6元 | 5元 | 4元 |
若小强购买香蕉x千克（x大于40千克）付了y元，则y关于x的函数关系式为 。
二、精心选一选（本题每小题4分，共32分）
1、骆驼被称为“沙漠之舟”，它的体温随时间的变化而变化，在这一问题中，因变量是（ ）
A、沙漠 B、体温 C、时间 D、骆驼
2、长方形的周长为24cm，其中一边为
（其中
），面积为
，则这样的长方形中与的关系可以写为（ ）
A、
B、
C、
D、
3．函数
的自变量x的取值范围为
（ ）
A．x≠1 B．x＞－1 C．x≥－1 D．x≥－1且 x≠1
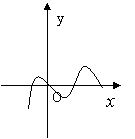
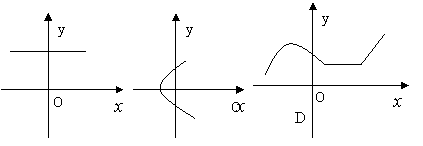
4．下列各图象中，y不是x函数的是 （ ）
 |  | ||
|
|
|
5．小明一出校门先加速行驶，然后匀速行驶一段后，在距家门不远的地方开始减速，而最后停下，下面哪一副图可以近似地刻画出以上情况：( )
A B C D
速度 速度 速度 速度
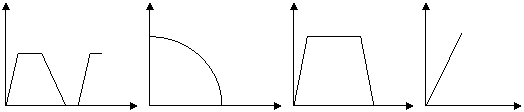
时间 时间 时间 时间
|
| 50 | 80 | 100 | 150 |
|
| 25 | 40 | 50 | 75 |
6． 表格列出了一项实验的统计数据，表示皮球从高度
落下时弹跳高度
与下落高的关系，试问下面的哪个式子能表示这种关系（单位
）（
）
、
、
、
、
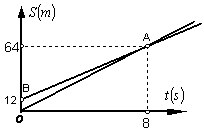7．如图所示，OA、BA分别表示甲、乙两名学生运动的路程与时间的关系图象，图中
和
分别表示运动路程和时间，根据图象判断快者的速度比慢者的速度每秒快（ ）
A、2.5
B、2
C、1.5 D、1
8．水池有2个进水口，1个出水口，每个进水口进水量时 间的关系如图甲所示，出水口水量与时间的关系如图乙所示．某天0点到6点，该水池的蓄水量与时间的关系如图丙所示.
下面的论断中：①0点到1点，打开两个进水口，关闭出水口；②1点到3点，同时关闭两个进水口和一个出水口；③3点到4点，关闭两个进水口，打开出水口； ④5点到6点，同时打开两个进水口和一个出水口．可能正确的是 （ ）
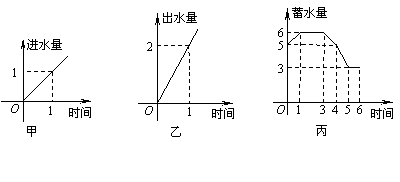
A．① ③ B．②④ C．① ④ Ｄ．②③
三、细心解一解（本题共4题，共36分）
1．如图，在靠墙（墙长为18m）的地方围建一个矩形的养鸡场，另三边用竹篱笆围成，
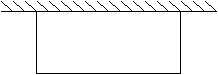如果竹篱笆总长为35m，求鸡场的长y （m）与宽x （m）的函数关系式，并求自变量的取值范围。
2．下列是三种化合物的结构式及分子式，
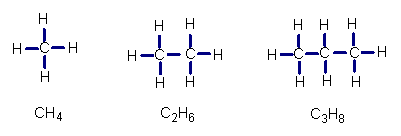
结构式
分子式
（1）请按其规律，写出后一种化合物的分子式 ．
（2）每一种化合物的分子式中H的个数m是否是C的个数n的函数？如果使写出关系式。
3．如图，反映了小明从家到超市的时间与距离之间关系的一幅图.
(1)图中反映了哪两个变量之间的关系？超市离家多远？
(2)小明到达超市用了多少时间？小明往返花了多少时间？
(3)小明离家出发后20分钟到30分钟内可以哪里？
(4)小明从家到超市时的平均速度是多少？返回时的平均速度是多少？
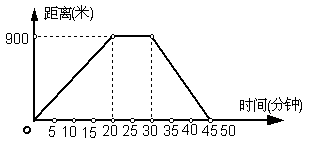
4．打市内电话都按时收费，并于200l年3月21日起对收费办法作了调整，调整前的收费办法：以3分钟为计时单位（不足3分钟按3分钟计），每个计时单位收0.2元；调整后的收费办法：3分钟内（含3分钟）0.2元，以后每加1分钟加收0.1元。
（1）根据调整后的收费办法，求电话费y（元）与通话时间t（分）之间的函数关系式（t＞3时设t（分）表示正整数）。
①当t
3时，y=
；
②当t＞3时（t（分）表示正整数），y= 。
（2）对（1），试画出0＜t6时函数的图象。
（3）就0＜t6，求t为何值时，调整前和调整后的电话费相同，并求出其相应的收费y（元）。
答案：
一、
1．x，y，90 2 x≥3
3. 列表法、图象法、解析法
4.4
5 .列表、描点、连线
6.0 7 增大 8.y=4x（x＞40）
二、
CCDCC DCC
三
1、y= -2x+35（0＜x＜9.5
2、C4H10 m=2n+2
3、（1）距离；时间，900m
（2）20分，45分
(3)在商场
（4）45米/分，60米/分
4、（1）①0.2②0.1t-0.1
(3)当0<t<3时， y=0.2,
当4<t≤5时,y=0.4