初二数学上期第一次月半考试卷
考试内容：第11章—第13章 本卷满120分 时间：90分钟
命题人：宁飞鸾
一、 认认真真选,沉着应战!（3分×10=30分）
1、为下面问题选择适当的统计图描述数据：反映某种股票的涨跌情况，应选择（ ）
A、条形统计图 B、折线统计图 C、扇形统计图 D、直方图
2、已知△ABC≌CDA，则它的一组对应边是（ ）
A、AB=BC B、AC=AB C、AD=CB D、AD=DC
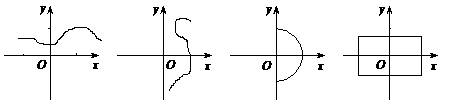3、下列图象中，表示y是x的函数的是（ ）
（A） （B） （C） （D）
4、若
是正比例函数，则b的值是 （ ）
| |
C.
D.
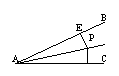5、如图所示,点P是∠BAC内的一点,且P到AB\、AC的距离PE=PF，则△PEA≌△PFA的理由是（ ）
|
6、在函数
中取不同的b值，可以得到不同的直线，那么这些直线必定（ ）
（A）交于一个点． （B）互相平行． （C）有无数交点． （D）不能确定．
7、 如下图所示，下列各图形中，是全等形的是（ ）
A、a,b,c,d都全等 B、a,b,c全等 C、b,c,d全等 D、a,c,d全等
8、有下列说法：①全等三角形的形状相同；②全等三角形的周长和面积相等；③若两个钝角三角形全等，则钝角所对的边是对应边；④两个全等形不论怎样改变位置，都能够完全重合。其中正确说法的个数是（ ）
A、1个 B、2个 C、3个 D、4个
9、频数、频率、数据的总个数，满足的关系式是（ ）
A、频率＋频数=数据的总个数 B、频率÷频数=数据的总个数
C、频数÷频率=数据的总个数 D、数据的总个数÷频率=频数
10、一次函数
与
，它们在同一坐标系中的大致图象是（ ）
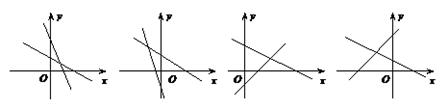
（A） （B） （C） （D）
二仔仔细细填,记录自信!（3分×8=24分）
11、在整数11122中，数字1出现的频率分别为____________。
12、已知点A(x1，y1)和点B(x2，y2)在同一条直线y=kx+b上，且k＜0。若x1＞x2，则y1与y2的大小关系是___________.
13、在一幅扇形统计图中，一扇形的圆心角为126 0 ，则该扇形的百分比为___________.
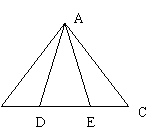
14、如下图D、E是△ABC中BC边上的两点，AE=AD，∠B=∠C、要证明△ABE≌△ACD，还应补充的条件为__________________.
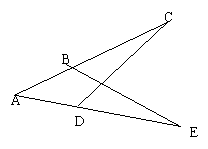
15、如下图，已知AD=AB，∠C=∠E，∠CBE=500 ，则∠ADC=_______________.
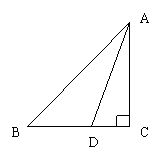
16、如下图，在△ABC中，∠C=900 ，AD平分∠BAC，交BC于D，若CD=5cm，则点D到AB距离为_________________.
|
|
|
|
17、函数y=
自变量的取值范围_____________________.
 |
18、有边长为1的等边三角形卡片若干张,使用这
些三角形卡片拼出边长分别是2、3、4…的等边
三角形(如图).根据图形推断每个等边三角形卡片
总数S与边长n的关系式 。
三、平心静气做,展示智慧!
19．已知
与x成正比例，且
2时，
4．
求出y与x之间的函数关系式.(6分)
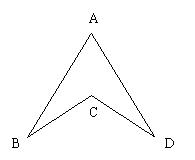20．如图，已知AB=AD，CB=CD，求证∠B=∠D（6分）
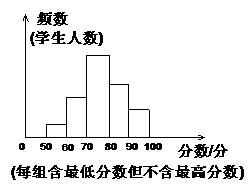
21、某班同学参加环保知识竞赛，将学生成绩（得分都是整数）进行整理后分成5组，绘成频数分布直方图（如图），图中从左到右各小长方形的高的比为1：3：6：4：2，最后一组的频数为6，结合直方图提供的信息解答下列问题：
（1）该班有多少名同学参赛？
（2）成绩落在哪组数据范围内的人数最多？是多少？
（3）求成绩在60分以上（含60分）的学生占全班参赛学生人数的百分率？
（4）大致估计该班级的平均分？
（5）请你直接在直方图的基础上绘制频数折线图？（10分）
 |
22.已知，直线y=2x+3与直线y=-2x-1.
（1）求两直线与y轴交点A，B的坐标;
（2）求两直线交点C的坐标;
（3）求△ABC的面积.(8分)
23、如图，BD为∠ABC的平分线，AB=BC，点P在BD上，PM⊥AD于M，PN⊥CD于N.
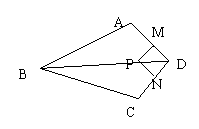求证：PM=PN.(8分)
24、甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球，乒乓球拍每付定价20元，乒乓球每盒定价5元，现两家商店搞促销活动，甲店：每买一付球拍赠一盒乒乓球；乙店：按定价的9折优惠，某班级需购球拍4付，乒乓球若干盒（不少于4盒）
（1）设购买乒乓球盒数为ｘ（盒），在甲店购买的付款数为ｙ甲（元）；在乙店购买的付款数为ｙ乙（元），分别写出ｙ甲、ｙ乙与ｘ的函数关系式。
（2）就乒乓球的盒数讨论去哪家商店购买合算？(8分)
25．如图，在正方形ABCD中，E是AD的中点，F是BA延长线上一点，AF=1／2AB,已知△ABE≌△ADF.(10分)
(1)在图中,可以通过平移、翻折、旋转中哪一种方法，使△ABE变到△ADF的位置；
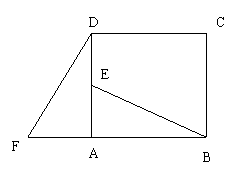（2）线段BE与DF有什么位置关系？证明你的结论