初二数学综合试题（13）
一.选择题(共30分每小题3分)
( )1. 的算术平方根为
A ± B ± C D
( )2. 的值为
A 8 B 4 C ±8 D ±4
( )3.如果两个相似三角形的对应中线的比为1: 2,则对应高线的比为
A 1 : 2 B 1 : 3 C 1 : 4 D 1 :
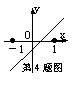( )4.函数y = a x + b 的图象如右下图所示:则下列式子有意义的为
A B C D
( )5.若斜坡AB的坡度为1: ,则坡角为
A 300 B 450 C 600 D 750
(
)6.如图,张村和李村要在河边修一提灌站P,现知道张村和李村离河边最近距离分别为1km和2km,且两个最近距离点相距4km,则两村至少需要的水管的长为多少千米?
A 3 B 4 C 5 D 6
( )7.在装有1个白球和3个黑球的袋子中摸球，搅匀后先摸出1个，放回搅匀，然后再摸出1 个，两次摸到哪种球的机会最大
A黑球 B一黑一白 C都一样 D无法确定
( )8.已知点A（2，－4）是正比例函数图象上的一点，则其函数解析式为
A y = 2x B y = C y = －2x D y = －
( )9.函数y = 2 x －3一定不经过的象限为
A 第一象限 B 第二象限 C 第三象限 D 第四象限
( )10.如图,在△ABC中,D为AB边上一点,在①∠1=∠B;
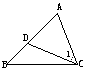②∠ADC=∠ACB;③AC2 =
AD·AB;④AC·BC= AB·CD
中,能断定△ACD～△ABC的条件是
A ①②③ B ①②④
C ①③④ D ①②③④
二.填空题(共30分每小题3分)
11.计算: 的平方根为 ;
12.比较大小:
13.两个相似三角形的最小边分别为2和3,且周长的差为12,则周长的和为 .
14.数1、2、3的第四比例项为
；
2和8的比例中项为 .
15.如右图所示,阴影部分的面积为 .
16.计算: 2sin300 +cos450 + cot600 = .
17.甲,乙两名射击选手,分别各射靶10次,各命中的环数如下:
甲：8 、9、10、9、8、10、9、9、10、8
乙：10、8、9、9、9、8、10、9、9、9
在这两选手中，方差最小的是 （甲、乙），最小为 ；
其中射击最稳定的选手为
。
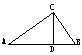
18.已知:如图,在△ABC中,∠ACB= 900 ,
CD⊥AB于D,AD = 4,BD = 1,则BC的长为 .
19.函数y = (2 k －1)x + 2中，y随x的增大需减小，则k的取值范围为
.
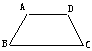
20.如图,在梯形ABCD中,AB = CD,AD∥BC
∠B=600,AB = 2,BC = 4,则S梯形ABCD=
三．解答题（共60分）
21.(5分)计算: 2+ 3－3
22.(5分)计算: 2sin600 －3tan300 + tan510·tan390
23.(10分)已知双曲线y = 与直线y = 2kx + b都经过点(1,2),求这两个函数的解析式.并在给定的坐标系内作出这两个函数的图象.
 |
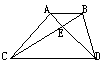
24.(8分) 如图，梯形ABCD中，AB∥CD，对角线BD，AC交于点E，问△AED与△BEC是否相似？有一位同学这样解答：
解:∵AB∥CD ∴∠ABE=∠CDE，∠BAE=∠DCE
∴△AEB∽△CED ∴= ∵∠AED=∠BEC
∴△AED∽△BEC
请判断这位同学的解答是否正确？如果不正确，请写出不相似的理由。（可将原解答稍作改正后抄下来）
 |
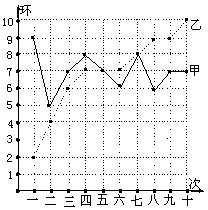
25.(10分) 甲乙两人在相同条件下各射靶10次，成绩如图。
(1)请将右表补充完整;
(2)请从方差、平均数走势看，谁的成绩更好；
(3)从折线图看谁更有实力？
| 平均数 | 方差 | 中位数 | 9环以上数 | |
| 甲 | 7 | 1.2 | 1 | |
| 乙 | 5.4 |
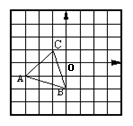
26.(10分)将图中的△ABC作下列运动，画出相应的图形，并写出运动后三个顶点的坐标及相应坐标所发生的变化。
(1)将△ABC沿x轴水平向右平移了3个单位得到△A1B1C1；
(2)将△ABC作关于x轴对称△A2B2C2。
27.(12分) 如图，在△OAB中，O为坐标原点，横、纵轴的单位长度相同，A、B的坐标分别为(8，6)，(16，0)，点P沿OA边从点O开始向终点A运动，速度每秒1个单位，点Q沿BO边从B点开始向终点O运动，速度每秒2个单位，如果P、Q同时出发，用t(秒)表示移动时间，当这两点中有一点到达自己的终点时，另一点也停止运动。
求(1)几秒时PQ∥AB
(2)作PC⊥BO于C,用t的代数式表示PC的长;（提示：必要时可作AD⊥BO于D）
(3)设△OPQ的面积为y，求y与t的函数关系式
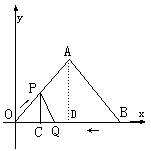
(4)△OPQ与△OAB能否相似，若能，求出点P的坐标，若不能，试说明理由
