初二数学综合检测题——整式

第十五章 初二数学综合检测题 —— 整式

一．选择题

1、下列运算正确的是（　　）

A　　　B　　　　C　  　 D　

2、在代数式、、、-5、a　中，单项式的个数是（　　 ）个

A. 1　　　　　  　　B. 2　　　　　  　　 C. 3　　　 　　　　　 D. 4

3、下列运算中，正确的是（　　）

A.　　 　B.  　C.　 　　　D.

4、若时，代数式的值为5，则时，代数式的值等于（　　）

A.0　　　 　　　　　B.－3 　 　　　　　　 C.－4　　　 　　　　 D.－5　

5、下列各式中，不能用平方差公式计算的是（　　 ）

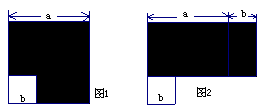
A．Ｂ．Ｃ．Ｄ．

6、下列各式计算正确的式子有（　　）

A．（２ｘ－６ｙ）²＝４x²－１２ｘy＋３６ｙ² Ｂ．（2x＋６）（x－６）²＝2x²－3６

C.（－ｘ－２ｙ）²＝x²－４ｘy＋４ｙ²  Ｄ．（ａ＋２ｂ）²＝ａ²+４ａｂ＋４ｂ^２

7、下列计算正确的是（　　 ）

A．（ －7x³－8x³+x）÷（－x）= 7x²－8x+1　　 B．　　　

　C．（x³+x⁴）÷x³=x⁴　　　　　　　　　　　　　 D． （3yⁿ-6xyⁿ⁺¹）÷yⁿ=3+2xy

8、下列从左边到右边的变形，是因式分解的是（　　 ）

　A、　　　　　　　　　  B、

　C、　　　　　  D、

9、下列多项式中能用平方差公式分解因式的是（　　 ）

　A、　　　　B、　　　 C、　　　　D、

10、△ABC的三边满足a²-2bc=c²-2ab，则△ABC是（　　）

　A、等腰三角形　　　　B、直角三角形　　　　 C、等边三角形　　　 D、锐角三角形

11、要在二次三项式x²+□x-6的□中填上一个整数，使它能按x²＋（a＋b）x＋ab型分解为（x＋a）（x＋b）的形式，那么这些数只能是　（　　）

A．1，-1；　 　　　　B．5，-5；　　　　　  C．1，-1，5，-5；　　D．以上答案都不对

12、已知a=2002x+2003，b=2002x+2004，c=2002x+2005，则多项式a²+b²+c²-ab-bc-ca的值为（　）

　A、0　　　　　　　　 B、1　　　　 　　　　 C、2　　　　　 　　　D、3

13、已知为三角形三边，且满足则这个三角形为（　 ）

　A.等腰三角形　　　　 B.直角三角形　　　　 C.等边三角形　　　D.等边三角形或直角三角形

二．填空题

14、单项式的系数是　　　　  ; 多项式是　　　 次　　　 项式.

15、若与是同类项，则＝　　　　  ；

16、如果单项式与是同类项，那么这两个单项式的积是　　　　　　 .

17、计算=　　　　  . =　　　　　 .

18、计算：＝　　　 　　 .

19、满足的所有x的个数有　　　　  个。

20、若a^m=8，aⁿ=32，则a^2m+n=　　　　  ；

21、计算：（x+1）（x-1）（x²-1）=　　　　　　　 。

22、.

23、计算：5a²b²c÷（－4ab²）=　　　　　  .

24、　　　　　

25、利用右图可以验证哪个乘法公式？用式子表示为　　　　　　  。

26、月球距离地球大约千米，一架飞机的速度约为千米/时，若乘飞机飞行这么远的距离，大约需要　　　　 天。

27、一个正方形的边长增加了，面积相应增加了，则这个正方形的边长为　　㎝

28、已知：，那么的值为_____________.

29、分解因式:m²a-4ma+4a=_________________________.

30、分解因式:＝_______________________.

31、观察右图，根据图形面积的关系，便可以得到一个用来分解因式的公式是　　　　　　　  .

32、已知为非负整数，且，则___________.

33、若=，则p=　　　,=　　　　  .

34、　　　　　 .

35、已知，则　　　　  .

36、已知，则=　　　　　  ；已知则＝　　　　 .

37、如果是一个完全平方式，那么=　　　　  .

38、化简：＝　　　　   

39、若代数式，其中，则的大小关系是 　　 。

40、若，则＝　　　　，＝　　　　  .

三．解答题

41、计算：

（1） （2）－3x³y·2x²y² （3）

（4）　　　（5）  （6）（-2a³b²c）³ 



（7） (6a⁵－7a²+36a³)÷3a²　　　　  （8）(－8a⁴b⁵c÷4ab⁵)·(3a³b²)　　 （9）

（10）　　 （11）　　

（13）　　　　　　　　　　　 （14）

（15）(2x＋y＋z)(2x＋y－z)　　　　　　　　　 （16）

（17）　　　　　 　　　　　　　　　 （18）

（19）  （20）

42、已知，求3A－2B

43、先化简，再求值：

（1），其中

（2）(3a-2b)(2a-b)-(2a-b)²-(2a+b)(2a-b)　 其中a=-1，b=2.

（3）,其中.

44、解方程（2x+3）(x-4)-(x-3)(x+2)=x²+6

45、把下列各式分解因式：



 



（5）　　　　　　　　　　  （6）

（7）　　　　　　　　 （8）

（9）　　　　　　　　　 （10）

（11）　　　 　　　　　　　 （12）

（13）　　　　  （14） (1)；

（15）　　　　　  （16）

（17）　　（18）

（19）　　　　　　　　　　　　　 （20）

（21）　　　　　　　  （22）

（23）　　　　　　　　　　　 （24）

46、已知：的值。

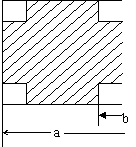
47、如图，在一块边长为a厘米的正方形纸板四角，各剪去一个边长为

　b(b<)厘米的正方形，利用因式分解计算当a=13.2，b=3.4时，剩余

部分的面积。

48、求证:a、b为任意值时,4a²+b²-8a+2b+6的值恒为正.

49、已知数a，b满足求的值.

50、已知，求的值。

 

 

51、已知展开后不含的项，求的值.

 

 

52、阅读材料并解答问题：

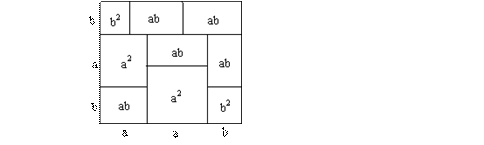我们已经知道，完全平方公式可以用平面几何图形的面积来表示，

实际上还有一些代数恒等式也可以用这种形式表示。

（1）请写出图3所表示的代数恒等式：

　　　　　　　　　　　　　　　 ；

（2）试画一个几何图形使它的面积能表示成：