初二数学— 一次函数测试卷
时间:90分钟 满分:100分
班级_______________姓名___________________成绩______________________
一、填空题（每题2分，共20分）
1.在圆的周长公式C=2πr中，变量是________，常量是_________.
2.函数
中自变量x的取值范围是___________.
3.已知一次函数
+3,则
= .
4.已知一次函数
,函数
的值随
值的增大而增大,则
的取值范围是 .
5.若函数
图象经过点（1，2），则m=
.
6.分别用x和y表示等腰三角形的顶角和底角的度数, y与x之间的函数解析式为____.
7.有边长为1的等边三角形卡片若干张,使用这些三角形卡片拼出边长分别是2、3、4…的等边三角形(如图).根据图形推断每个等边三角形卡片总数S与边长n的关系式 .
8.一次函数y= -2x+4的图象与x轴交点坐标是 ，与y轴交点坐标是
图象与坐标轴所围成的三角形面积是 .
9.写出同时具备下列两个条件的一次函数表达式（写出一个即可） .（1）y随着x的增大而减小。 （2）图象经过点（1，-3）
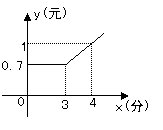10.在某公用电话亭打电话时，需付电话费y（元）与通话时间 x（分钟）之间的函数关系用图象表示如图.小明打了2分钟需付费______元；小莉打了8分钟需付费_______元.
(第7题图) (第10题图)
二、选择题
1．下列函数（1）y=πx (2)y=2x-1 (3)y= (4)y=2-3x (5)y=x2-1中，是一次函数的有（ ） （A）4个 （B）3个 （C）2个 （D）1个
2．已知点（-4，y1），（2，y2）都在直线y=- x+2上，则y1 y2大小关系是( )
（A）y1 >y2 （B）y1 =y2 （C）y1 <y2 （D）不能比较
3.下列给出的四个点中，不在直线y=2x-3上的是 （ ）
A.（1， -1） B.（0， -3） C.（2， 1） D.（-1，5）
4.某兴趣小组做实验，将一个装满水的啤酒瓶倒置（如图），并设法使瓶里的水从瓶中匀速流出。那么该倒置啤酒瓶内水面高度
随水流出的时间
变化的图象大致是
（
）
 | |||||||
 |  |  | |||||
A. B. C. D.
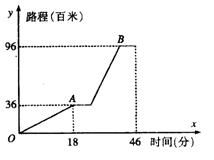5.某学校组织团员举行申奥成功宣传活动，从学校骑车出发，先上坡到达A地后，宣传8分钟；然后下坡到B地宣传8分钟返回，行程情况如图．若返回时，上、下坡速度仍保持不变，在A地仍要宣传8分钟，那么他们从B地返回学校用的时间是（ ）
A.45.2分钟 B.48分钟
C.46分钟 D.33分钟
6.若m＜0, n＞0, 则一次函数y=mx+n的图象不经过 （ ）
A.第一象限 B. 第二象限 C.第三象限 D.第四象限
7.若把一次函数y=2x－3,向上平移3个单位长度，得到图象解析式是( )
（A） y=2x (B) y=2x－6 （C） y=5x－3 （D）y=－x－3
8.已知函数
,当-1＜x≤1时，y 的取值范围是（ ）
A.
B.
C.
D.
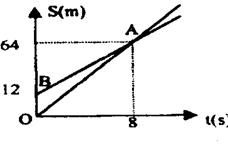9.如图，OA、BA分别表示甲、乙两名学生运动的一次函数，图中S和t分别表示运动路程和时间，已知甲的速度比乙快,下列说法:1射线BA表示甲的路与时间的函数关系;2甲的速度比乙快1.5米/秒;3甲让先跑了12米;48秒后,甲超过了乙,其中正确的说法是 （ ）
A. 12 B. 234
C. 23 D. 134
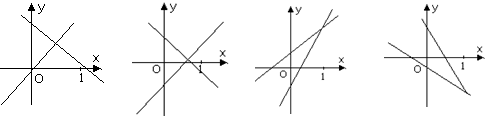
10.当
时，函数y=ax+b与
在同一坐标系中的图象大致是（ ）
 |
A. B. C. D.
三、解答题
1.（8分）已知直线
经过点（1，2）和点（
，4），求这条直线的解析式.
 |
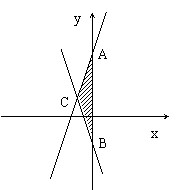2、已知，直线y=2x+3与直线y=－2x－1.
（1） 求两直线与y轴交点A，B的坐标;
（2） 求两直线交点C的坐标;
（3） 求△ABC的面积.
3、某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中含药量y与时间t之间近似满足如图所示曲线:
(1)分别求出
和
时,y与t之间的函
数关系式；
(2)据测定:每毫升血液中含药量不少于4微克
时治疗疾病有效,假如某病人一天中第一次服药
为7:00,那么服药后几点到几点有效?
４、某服装厂现有Ａ种布料70m，Ｂ种布料52m，现计划用这两种面料生产Ｍ、Ｎ两种型号的时装80套，已知做一套Ｍ型号的时装需要Ａ种布料0.6m，B种布料0.9m可获利索45元，做一套N型号的时装需要A种布料1.1m，Ｂ种面料0.4m,可获利50元，若设生产Ｎ型号的时装数为x，用这批布料生产这两种型号的时装所获的总利润为y元。
（１）求y与x的函数关系式，并求出自变量x的取值范围；
（２）该服装厂在生产这批时装中，当生产Ｎ型号的时装多少时，所获利润最大？最大利润是多少？
（附加题），
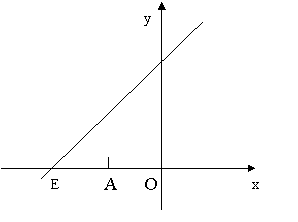如图，直线y=kx+6与x轴y轴分别交于点E，F. 点E的坐标为
(－８，０)，点Ａ的坐标为（－６，０）。（１）求k的值（２）若点p(x,y)是第二象限内的直线上的一个动点，当点P运动过程中，试写出△OPA的面积S与x的函数关系式，并写出自变量x的取值范围；（３）探究：当P运动到什么位置时，
△OPA的面积为
，并说明理由。