初二数学第一学期第一次月考试卷
本卷满100分 八年级数学 时间：120分钟 命题人：章云标 沈小兵
一、选择题（3分×12=36分）
1、为下面问题选择适当的统计图描述数据：反映某种股票的涨跌情况，应选择（ ）
A、条形统计图 B、折线统计图 C、扇形统计图 D、直方图
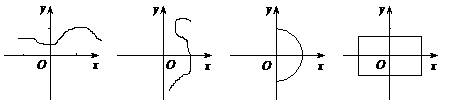2、下列图象中，表示y是x的函数的是（ ）
（A） （B） （C） （D）
3、若
是正比例函数，则b的值是 （ ）
A.0 B.
C.
D.
4、下列各点在函数
的图象上的是（ ）
（A）（
，
）． （B）（，4）． （C）（1，2）．
（D）（1，4）．
5、在函数
中取不同的b值，可以得到不同的直线，那么这些直线必定（ ）
（A）交于一个点． （B）互相平行． （C）有无数交点． （D）不能确定．
6、如图所示的世界人口扇形统计图中，关于中国 部分的圆心角的度数为（ ）
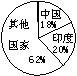A、64.8°
| |
C、72°
D、76°
7、据调查，某自行车存车处在某星期日的存车量为4000辆次，其中变速车存车费是每辆一次0.30元，普通车存车费是每辆一次0.20元．若普通车存车数为x辆次，存车费总收入为y元，则y关于x的函数关系式是（ ）
（A）
．
（B）
．
（C）
．
（D）
8、已知M（3，2），N（1，－1），点P在
轴上，且PM＋PN最短，则点P的坐标是（ ）
A、（0，
） B、（0，
） C、（0，0） D、（0，
）
9、已知，函数
，当自变量增加m时，相应的函数值增加（ ）
（A）
．
（B）
． （C）
． （D）
9、一次函数
与
，它们在同一坐标系中的大致图象是（ ）
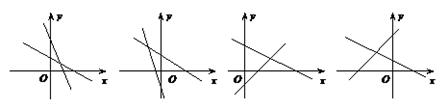
（A） （B） （C） （D）
11、已知点A(x1，y1)和点B(x2，y2)在同一条直线y=kx+b上，且k＜0。若x1＞x2，则y1与y2的关系是( )
A. y1＜y2 B.y1=y2 C. y1＞y2 D.y1与y2的大小不确定
12、若一次函数
的图像不经过第二象限，则
的取值范围是（ ）
A、＜ B、0＜＜
C、0≤＜ D、＜0或＞
二填空题（3分×5=15分）
13、在整数中，数字1出现的频率分别为____________。
14、某一次函数的图象经过点（
1，2），且函数y随自变量x的增大而减小，请你写出一个符合上述条件的函数关系式___________________。
15、已知一次函数y=(3-k)x-2k2+18, 当k= 时,它的图像经过原点。
16．直线y=k1x+4和直线y=k2x-1的交点在x轴上，那么k1：k2= 。
17.有边长为1的等边三角形卡片若干张,使用这
些三角形卡片拼出边长分别是2、3、4…的等边
三角形(如图).根据图形推断每个等边三角形卡片
总数S与边长n的关系式 。
18．函数
，它的图象与两坐标轴所围成的三角形面积为2，则b值为_______．
三、解答题（17～20每题7分，21题10分22题11分）
17．已知
与x成正比例，且
2时，
4．
（1）求出y与x之间的函数关系式； （2）设点（a，2）在这个图象上，求a；
（3）如果x的取值范围是0
5，求y的取值范围．
18、某班同学参加环保知识竞赛，将学生成绩（得分都是整数）进行整理后分成5组，绘成频数分布直方图（如图），图中从左到右各小长方形的高的比为1：3：6：4：2，最后一组的频数为6，结合直方图提供的信息解答下列问题：
（1）该班有多少名同学参赛？
（2）成绩落在哪组数据范围内的人数最多？是多少？
（3）求成绩在60分以上（含60分）的学生占全班参赛学生人数的百分率？
（4）大致估计该班级的平均分？
（5）请你直接在直方图的基础上绘制频数折线图？
 |
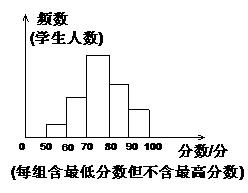
19.已知，直线y=2x+3与直线y=-2x-1.
（1）求两直线与y轴交点A，B的坐标;
（2）求两直线交点C的坐标;
（3）求△ABC的面积.
20．如图，lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
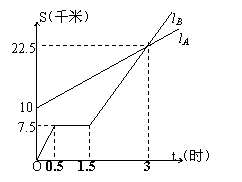（1）B出发时与A相距 千米。
（2）B走了一段路后，自行车发生故障，进行
修理，所用的时间是 小时。
（3）B出发后 小时与A相遇。
（4）若B的自行车不发生故障，保持出发时
的速度前进， 小时与A相遇，相遇点
离B的出发点 千米。在图中表示出
这个相遇点C。
（5）A行走的路程S与时间t的函数关系式 。
21、甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球，乒乓球拍每付定价20元，乒乓球每盒定价5元，现两家商店搞促销活动，甲店：每买一付球拍赠一盒乒乓球；乙店：按定价的9折优惠，某班级需购球拍4付，乒乓球若干盒（不少于4盒）
（1）设购买乒乓球盒数为ｘ（盒），在甲店购买的付款数为ｙ甲（元）；在乙店购买的付款数为ｙ乙（元），分别写出ｙ甲、ｙ乙与ｘ的函数关系式。
（2）就乒乓球的盒数讨论去哪家商店购买合算？
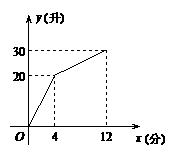22．有一个附有进出水管的容器，每单位时间内进出的水量都是一定的．设从某时刻开始的4分钟只进水不出水，在随后的8分钟内既进水又出水，得到时间x（分）与水量y（升）之间的关系如图所示．
（1）每分钟进水多少？
（2）当412时，x与y有何关系？
（3）若12分钟后，只放水不进水，求y的表达式．