八年级数学下学期期末模拟试题二
一、精心选一选(本大题共10小题，每小题4分，共40分。在每小题给出的四个选项中，只有一项是正确的，相信你一定会选对！)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1、下列四个函数中，在同一象限内，当x增大时，y值减小的函数是（ ）
A、y=5x B、
C、y=3x+2 D、
2、下列四组线段中，不构成比例线段的一组是（ ）
A、1cm, 2cm, 3cm, 6cm
B、2cm, 3cm, 4cm, 6cm,
C、1cm, 
cm, 
cm, 
cm,
D、1cm, 2cm, 3cm, 4cm,
3、不等式
的正整数解有（ ）
A.2个 B.3个 C.4个 D.5个
4、不等式组
的解集为（ ）
A.
≤x≤4 B.＜x≤4 C.＜x＜4 D.≤x＜4
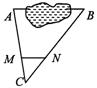5、如图，A、B两点被池塘隔开，在AB外任选一点C，连结AC、BC分别取其三等分点M、N量得 MN＝38m．则AB的长是
A. 152m
B.114m C.76m D.104m
6、下列各式从左到右的变形不正确的是（ ）
A.
B
.
C.
D.
7、已知△ABC中，∠ABC与∠ACB的平分线交于O，则∠BOC一定（ ）
A.小于直角 B.等于直角 C.大于直角 D.大于或等于直角
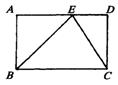
8、如图，在矩形ABCD中，点E是AD上任意一点，则有 （ ）
A．△ABE的周长＋△CDE的周长＝△BCE的周长 B、△ABE∽△DEC
C．△ABE的面积＋△CDE的面积＝△BCE的面积 D、△ABE∽△EBC
9、化简
的结果是（ ）
A.
B.
C.
D.
10、△ABC的三边之比为3：4：6，且△ABC∽△
，若△中最短边长为9，则它的最长边长为（ ）
A．21 B．18 C．12 D．9
二、细心填一填（本大题共10小题，每题4分，共40分。相信你会填对的！）
11、双曲线
经过点（3，k）则k＝
12、化简：
＝
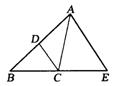
13、如图，CD平分∠ACB，AE∥DC交BC的延长线于点E，若∠ACE＝80°，则∠CAE＝
度．
14、已知关于x的不等式组
无解，则a的取值范围是________．
15、古希腊数学家 因其巨著《原本》而被后人誉为“几何学之父”．
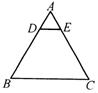
16、如图，在等边三角形ABC中，点D、E分别在AB、AC边上，且DE∥BC．如果BC＝8 cm，AD∶AB＝1∶4，那么△ADE的周长等于________ cm．
17、在比例尺为１：200
000的交通图上，距离为15厘米的两地之间的实际距离约为 千米．
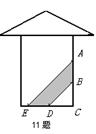
18、如图，阳光通过窗口照到室内，在地面上留下1．6m宽的亮区DE，已知亮区一边到窗下的墙脚距离CE=3．6m，窗高AB=1．2m，那么窗口底边离地面的高度BC= m ．
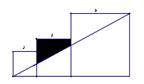19、已知三个边长分别为2、3、5的正方形如图排列，则图中阴影部分的面积为
20、盒子里装有大小形状相同的3个白球和2个红球，搅匀后从中摸出一个球，放回搅匀后,再摸出第二个球，则取出的恰是两个红球的的概率是___ ___．
三、认真答一答(本大题共7题，计70分。只要你认真思考，仔细运算，积极探索，一定会解答正确的！)
21、（10分）（1）计算：
（2）解方程：
22、（9分）小莉有红色、白色、蓝色上衣各一件，黄色、黑色长裤各一条。（1）有树状图分析小莉穿法的搭配情况；（2）小莉共有多少不同的穿法？（3）小莉穿黑色裤子的概率是多少？
23、（10分）如图，正方形ABCD的边长为5cm，用一块三角板，使它的一直角边始终经过点A，直角顶点E在BC上移动，另一直角边交CD于点F，如果BE＝x cm，CF＝y cm．
试用x的代数式表示y（不需要写出x的范围）．
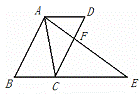
24、（8分）如图，ABCD是平行四边形，点E在边BC延长线上，连AE交CD于点F，如果∠EAC＝∠D．试证明：AC·BE＝AE·CD．
25、（9分）已知一次函数
的图象与反比例函数
的图象都经过点
，且点
又在一次函数的图象上．
（1）试求这两个函数的解析式；
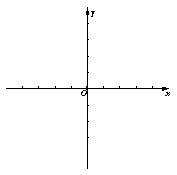
（2）在同一坐标系中画出这两个函数的图象，并说明在第二象限内，x取何值时，
；
（3）连结AO，BO，求△ABO的面积．（本题7分）
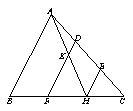26、（12分）如图△ABC中，D、E是AC上的三等分点，过D、E作DF∥AB，EH∥AB分别交BC于F、H，连AH交DF于K．
（1）求
的值；（2）求
的值；（3）求
的值．
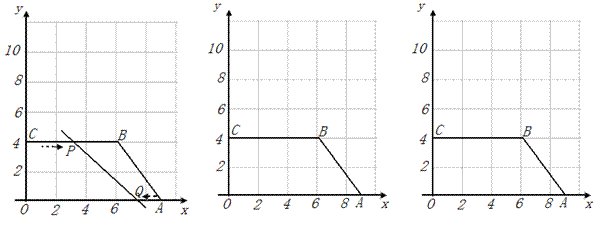
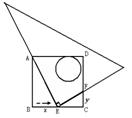
27、（12分）如图在平面直角坐标系中，已知直角梯形OABC的顶点分别是O（0，0），点A（9，0），B（6，4），C（0，4）．点P从点C沿C—B—A运动，速度为每秒2个单位，点Q从A向O点运动，速度为每秒1个单位，当其中一个点到达终点时，另一个点也停止运动．两点同时出发，设运动的时间是t秒．
（1）点P和点Q 谁先到达终点？到达终点时t的值是多少？
（2）当t取何值时，直线PQ∥AB ？并写出此时点Ｐ的坐标．（写出解答过程）
（3）是否存在符合题意的t的值，使直角梯形OABC被直线PQ分成面积相等的两个部分？如果存在，求出t的值；如果不存在，请说明理由．
（4）探究：当t取何值时，直线PQ⊥AB ?（只要直接写出答案，不需写出计算过程）．
