八年级数学
第一学期期中试卷4
一、细心选一选：（每题3分，共30分）
1．如图（1）直线L1与L2被L3所截，则∠1与∠2是（ ）
A．同位角 B．内错角
C．同旁内角 D．以上都有可能
2．如图（2）所示，下列说法中正确的是（ ）
A．若AB∥CD，则∠1=∠2 B．若AD∥BC，则∠3=∠4
C．若∠1=∠2，则AB∥CD D．若∠1=∠2，则AD∥BC
3．一天，小明的爸爸送给小明一个礼物，小明打开包装后，利用所学的知识，画出视图，它的主视图和俯视图分别如下图（3）
|
|
根据小明所画的两个视图，你知道小明爸爸送给小明小礼物是什么吗（ ）
A．钢笔 B．生日蛋糕 C．光盘 D．一套衣服
4．下列数据不能作为直角三角边长的是（ ）
A．3、4、5 B．7、24、25 C．6、8、10 D．6、11、12
5．数学老是布置10道选择题，课代表将全班同学的答题情况给制成条形统计，如图（4）根据图表，全班每位同学答题数的中位数和众数分别为（ ）
A．20，18 B．8，9
C．9，9 D．9、8
6．等腰三角形的两边长分别为4、6，则这个等腰三角形的周长为 （ ）
A．14 B．16 C．14或16 D．以上都不对
7．如图（5）是一个正方体纸盒展开图，每个面上都标柱了字母或数字，则面a在展开前所对的面的数字为（ ）
A．2 B．3
C．4 D．5
8．下列叙述中正确的个数为（ ）
①等腰三角形的高线、中线和角平分线互相重合 ②等腰三角形两底角外角相等
③等腰三角形有且只有一条对称轴 ④有一个角为60º的等腰三角形是等边三角形
A．1个 B．2个 C．3个 D．4个
9．若∠1与∠2的两边分别平行，且∠1比∠2的倍少30º，则∠2为（ ）
A．30º B．70º C30º或70º D．100º
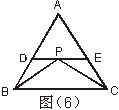
10．如图（6）所示，在△ABC中，AB=AC，PB和PC分别平分∠ABC和∠ACB，过P作DE∥BC交AB，AC于D、E，则图中共有等腰三角形的个数是（ ）
A．2个 B．3个
C．4个 D．5个
二、耐心填一填：（每题3分，共30分）
11．如图（7）已知L1∥L2，∠1=130º，则∠2= 。
12．请举出现实生活中两个直棱柱例子 、 。
13．已知等腰三角形顶角为36º，则底角为 。
14．已知直角三角形两直角边长分别为5cm、 12cm，则斜边上的中线为 cm.
15．评定学生的学科期末成绩，由期末分数，作业分数，课堂参与分数这三部分组成，并给予这三个部分权的比为3：3：4，已知小明期末考80分，作业90分，课堂参与85分，则他的数学期末成绩为 分。
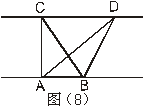
16．如图（8），已知直线AB∥CD，AC⊥AB，AB=3，AC=4，则△ABD的面积是 。
|
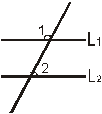
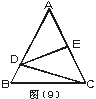
17．如图（9）在△ABC中，AB=AC=10，BC=8，DE为AC边上中垂线交AB于D，交AC于E，则△BDC的周长为 。
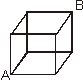
18．如图（10）边长为2厘米的立方体中，一只蚂蚁从顶点A出发沿着立方体的外表面爬到顶点B的最短路程是 。
|
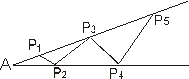
19．如图（11），钢条中，∠A=15º，焊上等长钢条，用来加固钢架，若P1A=P1B2问这样钢条至多需要 根。
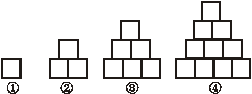
20．用边长为1cm的小正方形组成如图（12）塔状图案，则第n个图案的周长9是 。
|
三、用心做一做：（21、22每题6分，23题10分）
21．画图题：分别画出几何的主视图，左视图，俯视图。
主视图 左视图
俯视图
22．如图（13），已知△ABC中， B= ∠C，AE平分△ABC的外角∠CAD,判断,AE∥BC请说明理由。
解∵∠DAC是△ABC的一个外角（已知）
∴∠DAC=∠B+∠C（ ）
∵∠B=∠C（ ）
∴∠DAC=2∠B（等量代换）
∵AE是∠DAC的平分线（已知）
∴∠DAC=2∠ （ ）
∴∠B=∠
∴AE∥BC（ ）
23．八年级要举行投篮比赛，每班各30名，一名代表参加，根据在3分钟时间
内投中个数决出胜负，某班预选出甲、乙两位同学，在相同条件下，他们各投篮10次，每次投篮成绩情况如下表所示：
| 次 数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲（个） | 2 | 4 | 6 | 8 | 7 | 7 | 9 | 9 | 10 | 8 |
| 乙（个） | 9 | 5 | 7 | 8 | 7 | 6 | 6 | 7 | 7 | 8 |
（1）请填写下表：
| 平均数 | 方 差 | 中位数 | 中9个以上次数 | |
| 甲 | 7 | 5．4 | 1 | |
| 乙 | 7 |
（2）请从不同角度对这项测试结果进行分析；（至少写3条）
（3）如果你是班主任，你将选谁参加比赛？说说你的理由？
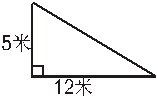
24．如图，一根竹竿，在离地面5米处断裂，竹竿顶部是在离竹竿底部12米处，问竹竿折断之前有多长？
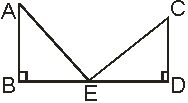
25．如图已知AB⊥BD于B，CD⊥BD于D，若AB=ED，BE=DC，则（1）AE=CE
（2）AE⊥CE请说明理由；
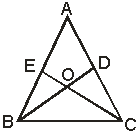
26．如图，已知△ABC中，D，E分别是AC，AB上的点，BD与CE相交于点O，给出下列三个条件：
①∠EBO=∠DCO ②∠BEO=∠CDO ③BE=CD
（1）上述三个条件哪两个条件可以判是△ABC为等腰三角形（用序号写出所有情形）
（2）选择第（1）小题中的一种情形，证明△ABC是等腰三角形。
