八年级数学第一学期期中质量检测试卷

八年级数学第一学期期中质量检测试卷

　 （时间：90分钟；总分110 分，超过100分以100分记）

2006年11月 　　　　　　　　　　　

一．　选择题（本题有10小题，共30分）．

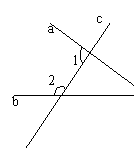
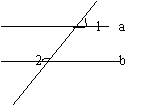
1．如右图，直线a，b被第三条直线c所截，

则∠1与∠2是（　　）

(A)同位角　(B)内错角　(C)同旁内角　(D)对顶角

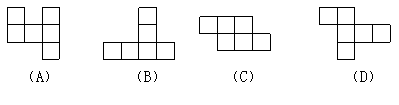
　2. 下列各图中能折成正方体的是(　　 )

3．下列语句中，正确的个数有（　 ）

①同位角相等　　 ②若两个角的和为180º，则这两个角是同旁内角

③两直线平行，同旁内角相等　  ④内错角相等，两直线平行

（A）、4个　　（B）、3个　　（C）、 2个　　 （D）、1个

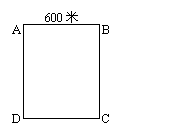
4．如图是长方形ABCD大理石广场示意图，已知AB=600米，如果小红

要从A角走到C角，至少走1000米，则BC的长为 （　　）

(A). 800米　 (B). 1000米　 (C). 1200米　  (D). 400米

（第4题图）

5．下列条件中，不能使两个直角三角形全等的条件是（　　）

（A）．斜边和一锐角对应相等　　 （B）．两直角边对应相等　

（C）．一锐角和一直角边对应相等 （D）．两锐角对应相等

6．在△ABC中，AB=15,AC=13,高AD=12,则三角形的周长是（　 ）

（A）42　　  (B)32 　　 (C)42或32　　  (D)37或33.

7．为了了解某地区15000名初中毕业生参加中考的数学成绩，从中抽取了500名考生的数学成绩进行统计分析，下列说法正确的是（　　 ）

　　（A）个体是指每个考生　　　　　　　　 （B）15000名考生是个体

　 （C）500名考生的成绩是总体的一个样本 （D）样本是指500名考生

年龄	13	14	15	16
人数	4	22	23	1

8．八年级（１）班５０名学生的年龄统计结果如表所示：

则此班学生年龄的众数、中位数分别为（　　 　　）

（A）．14，14  （B）．15，14　（C）．14，15　（D）．15，16

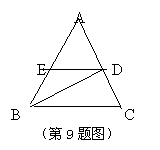
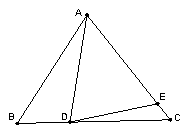
9．已知，如图在△ABC中，AB＝AC，∠A＝36°，BD是△ABC

的角平分线，DE∥BC，则图中等腰三角形的个数是（　　　　）

（A）．2　　　(B).3　　　(C).4　　　(D).5

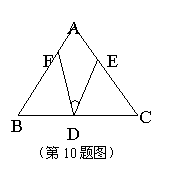
10．如图，在△ABC中，AB=AC，CD=BF，BD=CE，那么∠FDE

等于（　　）

（A）．90°-∠A　　　 （B）．90°+∠A　　

（C）．180°- ∠A　　　 （D）．90°-∠A

二．填空题：（本题有10小题，共30分）

11．如右图a∥b，∠1=45°，则∠2=　　　　　　  。

12．在△ABC中，AB=AC，∠A=50°，则∠B=　　　　　　　 。

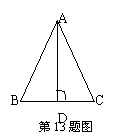
13. 如图,△ABC中，AD⊥BC于D，请你填上一个你认为合适的

条件：　　　　　　　　 使△ABD≌△ACD。

14．观察下列几组数：

①，，； ② 1，1，2 　③5，12，13　④6，7，8　⑤3，4，5

其中能作为直角三角形三边长的是：　　　　　　　（填序号）．

15．等腰三角形的两条边长是6和10，则它的周长是______.

16．在Rt△ABC中，∠C=90°，AB=15㎝，D是AB边的中点，

则CD=　　　　　 。

17．右图是某立体图形的平面展开图，请你写出它的名称：　　　　　　 。

18．等腰三角形的腰长为10，底边长为12，则此三角形的面积为______.

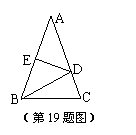
19．如图，在△ABC中，∠A=40º，AB=AC，AB的垂直平分线DE交AC

于D，则∠DBC的度数是　　　　　　　　　　．

20．小明帮助父母预算11月份电费情况，下表是11月初连续8天

每天早上电表的显示读数：

日　　期	1	2	3	4	5	6	7	8
电表显示读数	21	24	28	33	39	42	46	49

如果每度电费用是0.53元,请你估计小明家11月的电费是　　　　元.

三．解答题（21～24题，每题6分，25～26题，每题8分, 共40分）

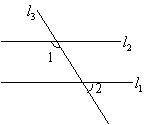21.如图，直线，被直线所截，∠1+∠2=180°，请说明直线与

平行的理由。

　　　　　　　　　　　　　　　　　　　　　 

22．画出下列几何体的三种视图。

23．如图，已知D是△ABC的BC边的中点，DE⊥AC，DF⊥AB，垂足分别为E，F，

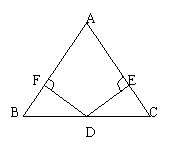且DF=DE，则△ABC是等腰三角形吗？请说明理由。

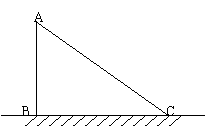24．受台风“麦莎”影响，有一根高为16米的电线杆BAC在A处折断，电线杆顶部C落在地面离电线杆底部B点8米远的地方，那么电线杆的断裂处A离地面的距离有多远？

25．某农科所为考察甲、乙两种小麦的长势，分别从中抽取10株苗，测得苗高如下（单位：cm）.

甲：9，10，11，12，7，13，10，8，12，8

乙：8，13，12，11，10，12，7，7，9，11

根据上述数据，请你回答下列问题：

（1）哪种小麦的10株苗长得比较高？

（2）哪种小麦的10株苗长得比较整齐？

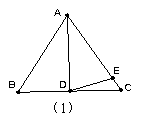
26．在ΔABC中，AB=AC

（1）如图1，如果∠BAD=30°，AD是BC上的高，AD=AE，则∠EDC=__________

　　　　 （2）如图2，如果∠BAD=40°，AD是BC上的高，AD=AE，则∠EDC=__________

　　　　 （3）思考：通过以上两题，你发现∠BAD与∠EDC之间有什么关系？请用式子表示：____________________

（4）如图3，如果AD不是BC上的高，AD=AE，是否仍有上述关系？如有，

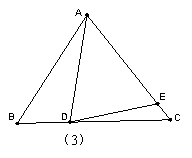
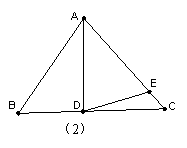请你写出来，并说明理由

四．选做题（第1题4分，第2题6分，共10分）

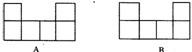1．桌面上摆着一些相同的正方体木块，主视图如图A所示，左视图如图B所示，要摆出这种形状，最多用______块木块，

最少有______块木块．

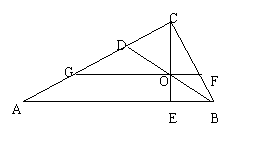
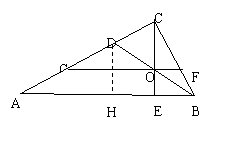
2．在RtΔABC中，∠C=90°，BD是∠ABC的平分线，交AC于D，CE是斜边AB上的高，E为垂足，CE交BD于O，过O作FG∥AB，交BC于F，AC于G，如图所示，

则CD和AG存在怎样的数量关系？并说明理由。

参考答案

一．选择题

1.C　2.D  3.D　4.A　5.D  6.C　7.C　8.B  9.D　10　10.D

二．填空题

11．135°; 12.65°;13.AB=AC(或∠B=∠C, ∠CAD=∠BAD等);

14. ①, ③, ⑤;　15.22或26 ; 16.7.5cm; 17.48; 18.长方体;

19.30°;20.63.6元

三．解答题

21.

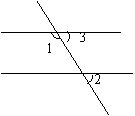解: ∵∠1+∠3=180°(平角的意义)

∠1+∠2=180°(已知)　　　　　　　　　 

∴∠2=∠3

∴∥(同位角相等,两直线平行)

22.

主视图　　　　　 左视图　　　　  俯视图

	解:∵D是△ABC的BC边的中点 　 ∴BD=CD　　　　　　　　　　 （1分） ∵DE⊥AC，DF⊥AB ∴∠BFD=∠CFD=Rt∠　　　　 （1分） 又∵DF=DE ∴Rt△BDF≌Rt△CDF(HL)　　　（2分） ∴∠B=∠C　　　　　　　　　  （1分） ∴△ABC是等腰三角形　　　　（1分）

23.

24.解：由题意得AB+AC=16，BC=8,∠ABC=90°；

设AB=x米,则AC=(16-x)米,根据勾股定理可得在Rt△ABC中，AB²+BC²=AC² ,所以x²+8²=(16-x)² ,解得x=6米

答: 电线杆的断裂处A离地面的距离有6米.

25．解: (1) ∵_甲=(9+10+11+12+7+13+10+8+12+8)÷10=10

　　　　 _乙=(8+13+12+11+10+12+7+7+9+11)÷10=10

　　　　 ∴从平均数来看两种小麦的10株苗长得一样高. （4分）

　　(2)S²_甲

=[(9-10)²+(10-10)²+(11-10)²+(12-10)²+(7-10)²+(13-10)²+(10-10)²+(8-10)²+(12-10)²+(8-10)²]=3.6

S²_乙

=[(8-10)²+(13-!0)²+(12-10)²+(11-10)²+(10-10)²+(12-10)²+(7-10)²+(7-10)²+(9-10)²+(11-10)² =4.2　　　　　　　　　　　　　　  （2分）

　∵S²_甲＜S²_乙

∴甲种小麦的10株苗长得比较整齐.　　　　　　　  （2分）

26．

(1)15°(2)20°(3)∠BAD=2∠EDC

(4) ∵AD=AE

∴∠ADE=∠AED

∵∠ADE+∠EDC=∠B+∠BAD

∠AED=∠EDC+∠C

∴∠EDC+∠C+∠EDC=∠B+∠BAD

∵AB=AC

∴∠B=∠C

∴2∠EDC =∠BAD

四．选做题

1.20;10

2.解:过点D作DH⊥AB,垂足为H,

在△BDH和△BDC中，

∵BD=BD

 ∠DBH=∠DBC

∠BHD=∠BCD=90°

∴△BDH≌△BDC

∴DH=DC （利用BD是∠ABC的平分线，由角平分线性质得此结论也可）

（1分）

又∵∠CDO=∠A+∠ABC　　∠COD=∠ECB+∠ABC

而∠A、∠ECB都是∠ABC的余角

∴∠A=∠ECB　　　　　　　　　　　　　　　　 

∴∠CDO=∠COD　　　　　　　　　　　　　　　　  （1分）

∴CD=CO

∴DH=CO　　　　　　　  （1分）

∵FG∥AB，CE⊥AB

∴CE⊥FG，∠CGO=∠A　　　（1分）

∴Rt△CGO≌Rt△DAH　　 （1分）

∴CG=DA

∴CD=AG　　　　　　　　　 （1分）